
分析 作AD⊥BC于D,根据直角三角形的性质和勾股定理求出BD、AD的长,根据三角形的面积=$\frac{1}{2}$×(AB+BC+AC)×r计算即可.
解答 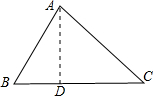 解:作AD⊥BC于D,
解:作AD⊥BC于D,
∵∠ABC=60°,
∴∠BAD=30°,∴BD=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴AD=$\frac{5\sqrt{3}}{2}$,CD=BC-BD=$\frac{11}{2}$,
∴AC=7,
设△ABC的内切圆半径为r,
$\frac{1}{2}$×(AB+BC+AC)×r=$\frac{1}{2}$×BC×AD,
解得,r=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查的是三角形内心的性质,掌握三角形的内心是三角形三条角平分线的交点和角平分线的性质是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2+2 | B. | y=(x-1)2-2 | C. | y=(x+1)2-2 | D. | y=(x+1)2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 买进20棵树苗与种树10棵 | |
| B. | 一辆出租车向北行驶24米与向南行驶15米 | |
| C. | 盈利50元与亏损40元 | |
| D. | 气温升高3℃与气温降低5℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
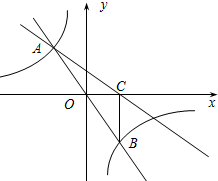 如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=$\frac{n}{x}$相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=$\frac{n}{x}$相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com