
分析 根据销售利润=销售量×(售价-进价),列出平均每天的销售利润w(元)与降价x元之间的函数关系式,依据二次函数性质最大利润.
解答 解:∵商品进价为每件40元,当售价为每件60元时,每星期可卖出300件,每降价1元每星期可多卖出20件,设每件降价x元,所得利润为W,则
W=(300+20x)(60-40-x),
=-20x2+100x+6000,
=-20(x-2.5)2+6125,
∴x=2.5时W=6125,
∴当降价2.5元时,w的最大值为6125元.
点评 此题主要考查了二次函数的性质在实际生活中的应用,最大销售利润的问题常利函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值在x=-$\frac{b}{2a}$时取得.


科目:初中数学 来源: 题型:解答题
| z(元/个) | 16 | 14 | 12 | 10 |
| y(个) | 120 | 180 | 240 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
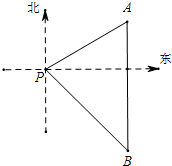 一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)
一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )
如图,上体育课,九年级三班的甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是( )| A. | 4米 | B. | 5米 | C. | 6米 | D. | 7米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com