
| z(元/个) | 16 | 14 | 12 | 10 |
| y(个) | 120 | 180 | 240 | 300 |
分析 (1)观察图表可得该函数图象是一次函数,设出一次函数解析式,把其中两点代入即可求得该函数解析式,进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同;
(2)根据销售利润=每个许愿瓶的利润×销售量列出函数表达式;令W=1200,解方程即可.
(3)根据进货成本可得自变量的取值,结合二次函数的关系式即可求得相应的最大利润.
解答 解:(1)y是x的一次函数,设y=kx+b图象过点(10,300),(12,240),
$\left\{\begin{array}{l}{10k+b=300}\\{12k+b=240}\end{array}\right.$,
解得
$\left\{\begin{array}{l}{k=-30}\\{b=600}\end{array}\right.$,
故y与x 之间的函数关系为:y=-30x+600,
当x=14时,y=180;当x=16时,y=120,
即点(14,180),(16,120)均在函数y=-30x+600的图象上.
∴y与x之间的函数关系式为y=-30x+600;
(2)w=(x-6)(-30x+600)=-30x2+780x-3600
即w与x之间的函数关系式为w=-30x2+780x-3600;
令W=1200,则-30x2+780x-3600=1200,
解得:x1=10,x2=16,
因为了方便顾客,所以售价定位为10元时可获利1200元.
(3)由题意得6(-30x+600)≤900,解得x≥15.
w=-30x2+780x-3600=-30(x-13)2+1350,
∵对称轴为x=13,a=-30<0,
∴抛物线开口向下,当x≥15时,w随x增大而减小,
∴当x=15时,w最大=1350.
即以15元/个的价格销售这批许愿瓶可获得最大利润1350元.
点评 此题主要考查了二次函数的最值问题、利用待定系数法求一次函数得解析式、掌握待定系数法求一次函数的解析式以及配方法求二次函数的最值是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.
已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
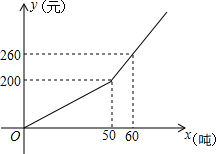 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com