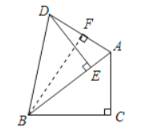
【题目】如图，Rt△ABC中，∠C=90°，把R△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上 .
(1)若∠BDA=70°，求∠BAC的度数；
(2)若BC=8，AC=6，求△ABD中AD边上的高.
【答案】（1）50° （2）
【解析】
（1）由旋转性质知BD=BA，∠CBA=∠EBD，据此可得∠BDA=70°，从而得∠ABD=∠ABC=40°，结合∠C=90°可得答案；
（2）由旋转性质得BE=BC=8，DE=AC=6，AB=BD=10，从而得AE=2，利用勾股定理知AD=
，作BF⊥AD于点F得AF=
AD=
，再次利用勾股定理可得答案．
解：(1)由旋转性质知BD=BA，∠CBA=∠EBD，
∵∠BDA=70°，
∴∠BAD=70°，
∴∠ABD=∠ABC=40°，
∵∠C=90°，
∴∠BAC=50°；
(2)∵BC=8，AC=6，∠C=90°，
∴AB=
=
=10，
由旋转性质知△ABC≌△DBE，
则BE=BC=8，DE=AC=6，AB=BD=10
∴AE=AB-BE=2，
在Rt△ADE中，AD=
作BF⊥AD于点F，
∵BA=BD，
∴AF=AD=
∴BF=
科目：初中数学 来源： 题型：
【题目】回答下列问题：
（1）如图所示的甲、乙两个平面图形能折什么几何体？
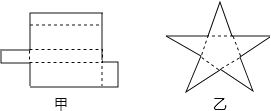
（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v﹣e的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．
查看答案和解析>>
科目：初中数学 来源： 题型：
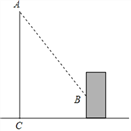
【题目】小左同学想利用影长测量学校旗杆的高度，如图，她在某一时刻立一长度为1米的标杆，测得其影长为
米，同时旗杆投影的一部分在地上，另一部分在某一建筑物的墙上，测得旗杆与建筑物的距离为10米，旗杆在墙上的影高为2米，请帮小左同学算出学校旗杆的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上，点A表示﹣10，点B表示11，点C表示18．动点P从点A出发，沿数轴正方向以每秒2个单位的速度匀速运动；同时，动点Q从点C出发，沿数轴负方向以每秒1个单位的速度匀速运动．设运动时间为t秒．
（1）当t为何值时，P、Q两点相遇？相遇点M所对应的数是多少？
（2）在点Q出发后到达点B之前，求t为何值时，点P到点O的距离与点Q到点B的距离相等；
（3）在点P向右运动的过程中，N是AP的中点，在点P到达点C之前，求2CN﹣PC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】《庄子·天下》：“一尺之棰，日取其半，万世不竭.”意思是说：一尺长的木棍，每天截掉一半，永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想，今天我们运用此数学思想研究下列问题.
（规律探索）
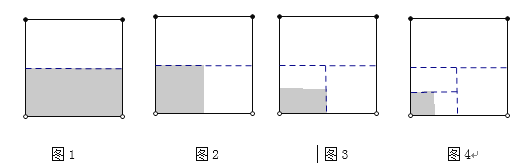
(1)如图1所示的是边长为1的正方形，将它剪掉一半，则S阴影1＝1－
＝__________；
如图2，在图1的基础上，将阴影部分再裁剪掉—半，则S阴影2＝1－－()2＝_______；
同种操作，如图3，S阴影3＝1－－()2－()3＝__________；
如图4，S阴影4＝1－－()2－()3－()4＝___________；
……
若同种地操作n次，则S阴影n＝1－－()2－()3－…－()n＝_________.
（规律归纳）
(2)直接写出＋
＋
＋…＋
的化简结果：_________.
（规律应用）
(3)直接写出算式＋＋＋…＋的值：__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如点M、N把线段AB分割成AM、MN、BN，若以AM、MN、BN，为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割点．
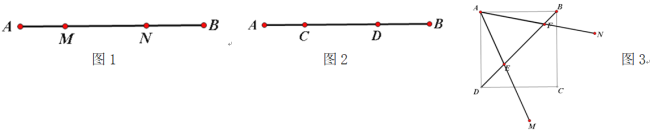
（1）如图2，已知点C、D是线段AB的勾股分割点，若AC=3，DB=4，求CD的长；
（2）如图3，在正方形ABCD中，∠MAM=45°，角的两边AM、AN分别交BD于E、F（不与端点重合），求证：E、F是BD的勾股分割点．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛（即每两个队之间比赛一场），一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军，为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜（ ）
A.10场B.11场C.12场D.13场
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
