
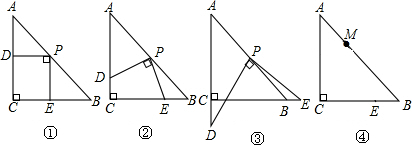
���� ��1����Ϊ��ABC�ǵ���ֱ�������Σ���������PC�����õ���ACP����CPB���ǵ���ֱ�������Σ�����CP���Ϳ���֤����CDP�ա�BEP���ٸ���ȫ�������εĶ�Ӧ����ȣ��Ϳ���֤��DP=PE��
��2����PBE�ܳ�Ϊ���������Σ�λ�������֣�
��3����MH��CB��MF��AC���������������Ρ�MDF�͡�MHE��Ȼ�����ö�Ӧ�߳ɱ������Ϳ������MD��ME֮���������ϵ��
���  �⣺��1�����ͼ1������PC��
�⣺��1�����ͼ1������PC��
�ߡ�ABC�ǵ���ֱ�������Σ�P��AB���е㣬
��CP=PB��CP��AB����ACP=$\frac{1}{2}$��ACB=45�㣮
���ACP=��B=45�㣮
�֡ߡ�DPC+��CPE=��BPE+��CPE=90�㣬
���DPC=��BPE��
���PCD�ա�PBE��
��PD=PE��
��2���������������
�ٵ���C���E�غϣ���CE=0ʱ��PE=PB��
��CE=2-$\sqrt{2}$����ʱPB=BE��
�۵�CE=1ʱ����ʱPE=BE��
�ܵ�E��CB���ӳ����ϣ���CE=2+$\sqrt{2}$ʱ����ʱPB=EB��
��3��MD��ME=1��3��
���ͼ2������M��MF��AC��MH��BC������ֱ���F��H��
��MH��AC��MF��BC��
���ı���CFMH��ƽ���ı��Σ�
�ߡ�C=90�㣬
��?CFMH�Ǿ��Σ�
���FMH=90�㣬MF=CH��
��$\frac{CH}{HB}$=$\frac{AM}{MB}$=$\frac{1}{3}$��HB=MH��
��$\frac{MF}{MH}$=$\frac{1}{3}$��
�ߡ�DMF+��DMH=��DMH+��EMH=90�㣬
���DMF=��EMH��
�ߡ�MFD=��MHE=90�㣬
���MDF�ס�MEH��
��$\frac{MD}{ME}$=$\frac{MF}{MH}$=$\frac{1}{3}$��
���� �����ۺϿ�����ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ε��ж������ʡ�ͼ�εı任���ۺ��Ժ�ǿ�����ɶ����ļ���Ҫ��Ҳ�Ƚϸߣ�


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
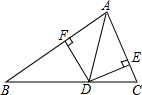 ��ͼ����D��BC���ϵĵ㣬DE��AB��E��DF��AC��F��AE=AF������AD����֪��ABD�����Ϊs1����ACD�����Ϊs2��BC=a��AC=b��AB=c��
��ͼ����D��BC���ϵĵ㣬DE��AB��E��DF��AC��F��AE=AF������AD����֪��ABD�����Ϊs1����ACD�����Ϊs2��BC=a��AC=b��AB=c���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
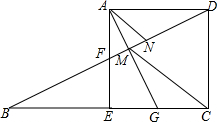 ��ͼ����������ADCE�У�FΪAE�е㣬DF��CE���ӳ�����B�㣬CM��AN����DF��M��N��
��ͼ����������ADCE�У�FΪAE�е㣬DF��CE���ӳ�����B�㣬CM��AN����DF��M��N���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com