
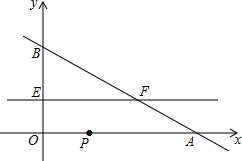
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-0.5x+2��������ֱ���A��B���㣬����P��A�����������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ2��1��$\sqrt{5}$�����ȵ�λ/�룩����Eͬʱ��O�������OB��$\frac{1}{3}$�����ȵ�λ/�룩���ٶ��˶���ֱ��EF��x�ύBA�ڵ�F�����˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ����P�͵�Eͬʱֹͣ�˶��������������⣺
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-0.5x+2��������ֱ���A��B���㣬����P��A�����������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ2��1��$\sqrt{5}$�����ȵ�λ/�룩����Eͬʱ��O�������OB��$\frac{1}{3}$�����ȵ�λ/�룩���ٶ��˶���ֱ��EF��x�ύBA�ڵ�F�����˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ����P�͵�Eͬʱֹͣ�˶��������������⣺���� ��1�����ȸ����ٶȡ�ʱ��=·�̣������P�˶���·���Ƕ��٣�������t��ʾ��P�ڲ�ͬ�߶��ϵ����ꣻȻ�����·�̡��ٶ�=ʱ�䣬�����P��ÿ���߶��ϵ��˶�ʱ�䣬���t��ȡֵ��Χ���ɣ�
��2���������E��F�Լ����ǵ��е�����ꣻȻ���жϳ����˶������У�����P��E��P�䣬F�γɵ��ı��������Σ����P��EF���е�ĺ�������ͬ���ݴ��жϳ�������t�Ƿ���ڼ��ɣ�
��3���������⣬������������ٵ���EFP=90��ʱ���ڵ���EPF=90��ʱ���۵���PEF=90��ʱ��������п��ܵ�ʱ��t��ʹ����P��E��F����Ϊ����������γ�Ϊֱ�������Σ�
��� �⣺��y=-0.5x+2��
��A��4��0����B��0��2����
��AB=$\sqrt{{4}^{2}{+2}^{2}}=2\sqrt{5}$��
��1���ٵ���P��AO���˶�ʱ��
��4��2=2���룩��
��0��t��2��
���P��AO�ϵ������ǣ�4-2t��0����0��t��2��
�ڵ���P��OB���˶�ʱ��
��2��1=2���룩��
��2��t��4��
���P��AO�ϵ������ǣ�0��t-2����2��t��4��
�۵���P��BA���˶�ʱ����ͼ1�� ��
��
��$2\sqrt{5}$��$\sqrt{5}$=2���룩��
��4��t��6��
���P��AO�ϵ������ǣ�4-2t��0����
��$\frac{CP}{OA}=\frac{BP}{BA}=\frac{\sqrt{5}��t-4��}{2\sqrt{5}}=\frac{t-4}{2}$��OA=2��
��CP=2��t-4��=2t-8��
��$\frac{DP}{BO}=\frac{AP}{AB}$=$\frac{2\sqrt{5}-\sqrt{5}��t-4��}{2\sqrt{5}}=\frac{6-t}{2}$��BO=2��
��DP=6-t��
���P��BA�ϵ������ǣ�2t-8��t-6����4��t��6��
��2��OE=$\frac{1}{3}t$��
��$\frac{1}{3}t=0.5x+2$��
���x=$\frac{2}{3}t-4$��
��F��$\frac{1}{3}t��\frac{2}{3}t-4$����
��EF���е�M��$\frac{1}{3}t-2��\frac{1}{3}t$����
�ٵ���P��AO���˶�ʱ����ͼ2�� ��
��
Ҫʹ���˶������У�����P��E��P�䣬F�γɵ��ı��������Σ�
��4-2t=$\frac{1}{3}t-2$��
���t=2$\frac{4}{7}$��
��2$\frac{4}{7}��2$��
�൱��P��AO���˶�ʱ��t�����ڣ�
�ڵ���P��BA���˶�ʱ����ͼ3�� ��
��
Ҫʹ���˶������У�����P��E��P�䣬F�γɵ��ı��������Σ�
��2t-8=$\frac{1}{3}t-2$��
���t=3.6��
��3.6��4��
�൱��P��BA���˶�ʱ��t�����ڣ�
���ϣ��ɵ�
������t��ʹ���˶������У�����P��E��P�䣬F�γɵ��ı��������Σ�
��3������ͼ4�� ��
��
����EFP=90��ʱ��
4-2t=$\frac{2}{3}t-4$��
���t=$\frac{1}{3}$��
����ͼ5�� ��
��
����EPF=90��ʱ��
$\frac{\frac{1}{3}t-0}{0-��4-2t��}•\frac{\frac{1}{3}t-0}{��\frac{2}{3}t-4��-��4-2t��}=-1$��
���t=$\frac{120��12\sqrt{2}}{49}$��
��$\frac{120+12\sqrt{2}}{49}��2��\frac{120-12\sqrt{2}}{49}��2$��
�����������t��
����ͼ6�� ��
��
����PEF=90��ʱ��
��P�˶�����O��
��ʱt=2��
���ϣ��ɵ�
��t=$\frac{1}{3}$��t=2ʱ����P��E��F����Ϊ������������ܷ��Ϊֱ�������Σ�
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������������Ĺؼ��ǣ�
��2������������г��������ٶȡ�ʱ���·�̵Ĺ�ϵ���ٶȡ�ʱ��=·�̣�·�̡�ʱ��=�ٶȣ�·�̡��ٶ�=ʱ�䣬Ҫ�������գ�
��3�����������ֱ�������ε����ʣ��Լ����ε����ʣ�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x+y=50}\\{10��x+y��=320}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
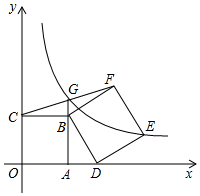 ��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC�������Σ���A��C������ֱ�Ϊ��2��0������0��2����D��x���������ϵ�һ�㣨��D�ڵ�A���ұߣ�����BDΪ��������������BDEF��E��F�����ڵ�һ���ޣ�������FC��AB���ӳ����ڵ�G��������������y=$\frac{k}{x}$��ͼ����E��G���㣬��k��ֵΪ5��
��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC�������Σ���A��C������ֱ�Ϊ��2��0������0��2����D��x���������ϵ�һ�㣨��D�ڵ�A���ұߣ�����BDΪ��������������BDEF��E��F�����ڵ�һ���ޣ�������FC��AB���ӳ����ڵ�G��������������y=$\frac{k}{x}$��ͼ����E��G���㣬��k��ֵΪ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
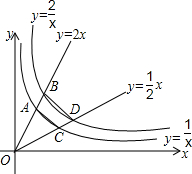 ��ͼ��ֱ��y=2x��y=$\frac{1}{2}$x�ֱ���˫����y=$\frac{1}{x}$��y=$\frac{2}{x}$�ڵ�һ���ķ�֧����A��B��C��D�ĵ㣬���ı���ABCD�����Ϊ$\frac{3}{4}$��
��ͼ��ֱ��y=2x��y=$\frac{1}{2}$x�ֱ���˫����y=$\frac{1}{x}$��y=$\frac{2}{x}$�ڵ�һ���ķ�֧����A��B��C��D�ĵ㣬���ı���ABCD�����Ϊ$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��p��q��b | B�� | $\frac{q}{p}$��$\frac{b}{a}$ | C�� | $\frac{1}{q}$��$\frac{1}{b}$��$\frac{1}{a}$��$\frac{1}{p}$ | D�� | $\frac{1}{a}$��$\frac{1}{p}$��$\frac{1}{q}$��$\frac{1}{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC������BD��CE���ڵ�O������OA����G��F�ֱ�ΪOC��OB���е㣬BC=8��AO=6�����ı���DEFG���ܳ�Ϊ��������
��ͼ����ABC������BD��CE���ڵ�O������OA����G��F�ֱ�ΪOC��OB���е㣬BC=8��AO=6�����ı���DEFG���ܳ�Ϊ��������| A�� | 12 | B�� | 14 | C�� | 16 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
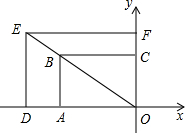 ��ͼ������OABC�����ODEF��λ��ͼ�Σ���OΪλ�����ģ����Ʊ�Ϊ1��1.2����B������Ϊ��-3��2�������E�������ǣ�������
��ͼ������OABC�����ODEF��λ��ͼ�Σ���OΪλ�����ģ����Ʊ�Ϊ1��1.2����B������Ϊ��-3��2�������E�������ǣ�������| A�� | ��3.6��2.4�� | B�� | ��-3��2.4�� | C�� | ��-3.6��2�� | D�� | ��-3.6��2.4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3m2•m=3m3 | B�� | ��2m��3=6m3 | C�� | ��a+b��2=a2+b2 | D�� | 3mn-3n=m |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com