
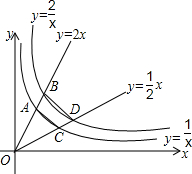
 如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$.
如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$. 分析 首先过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,过点C作CG⊥x轴于点G,过点D作DH⊥x轴于点H,根据直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,从而求得点A、B、C、D的坐标,则可由S△OAC=S△OAM+S梯形AMGC-S△OCG=S梯形AMGC,S△BOD=S梯形BNHD,求得△AOC和△BOD的面积,然后根据S四边形ABDC=S△BOD-S△OAC求得答案.
解答 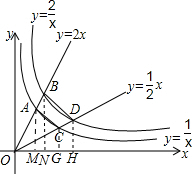 解:如图,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,过点C作CG⊥x轴于点G,过点D作DH⊥x轴于点H,
解:如图,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,过点C作CG⊥x轴于点G,过点D作DH⊥x轴于点H,
∵直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,
∴点A($\frac{\sqrt{2}}{2}$,$\sqrt{2}$),点B(1,2),C($\sqrt{2}$,$\frac{\sqrt{2}}{2}$),D(2,1)
∴S△OAC=S△OAM+S梯形AMGC-S△OCG=S梯形AMGC=$\frac{1}{2}$×($\sqrt{2}$+$\frac{\sqrt{2}}{2}$)($\sqrt{2}$-$\frac{\sqrt{2}}{2}$)=$\frac{3}{4}$,S△BOD=S梯形BNHD=$\frac{1}{2}$(2+1)(2-1)=$\frac{3}{2}$
∴S四边形ABDC=S△BOD-S△OAC=$\frac{3}{2}$-$\frac{3}{4}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题考查了反比例函数和一次函数的交点问题,根据S△OAC=S梯形AMGC,S△BOD=S梯形BNHD求得△AOC和△BOD的面积是本题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
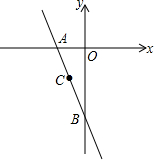 如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B
如图,直线y=kx+b经过点C(-1,-2),与x轴交于点A(-2,0),与y轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{4}$=2 | C. | $\root{3}{-64}$=-4 | D. | $\sqrt{{{{(-2)}^2}}}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE,其中正确的结论是( )| A. | 只有①③ | B. | 只有①③④ | C. | 只有②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
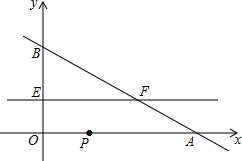 如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题:
如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
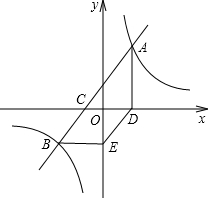 如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com