
【题目】三角形ABC中,∠ABC=105°,过点B作BD⊥AC,垂足为D,E是线段BC上一点,且∠BED=75°,F是射线BA上一点,过点F作FG⊥AC,垂足为G.若∠BDE=55°,则∠BFG=______.
【答案】125°或55°
【解析】
如图,分点F在BA边及BA边延长线上两种情况,根据三角形内角和定理求出∠DBE的度数,再求出∠DBF的度数,根据BD⊥AC,FG⊥AC可证明BD∥FG,利用平行线的性质可得出结论.
①当点F在BA边上时,如图1,
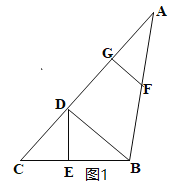
在△BDE中,∠BED=75°,∠BDE=55°,
∴∠DBE=180°-∠BDE-∠BED=180°-55°-75°=50°,
∵∠ABC=105°,
∴∠ABD=105°-50°=55°,
∵BD⊥AC,FG⊥AC,
∴BD∥FG,
∴∠ABD+∠BFG=180°,
∴∠BFG=180°-∠ABD=180°-55°=125°;
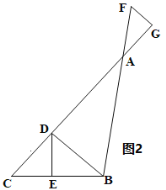
②当点F在BA边延长线上时,如图2,
同①可得∠ABD=55°,BD∥FG,
∴∠BFG=∠ABD=55°,
故答案为:125°或55°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
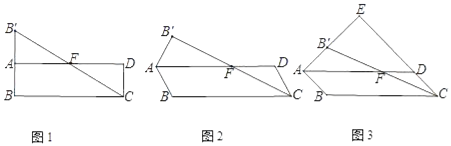
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
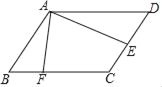
【题目】如图,在![]() ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=![]() ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=![]() ,则线段BF的长为__________.
,则线段BF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
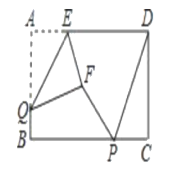
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是().
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D 则下列判断错误的是( )
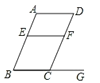
A.∠BEF=∠EFDB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

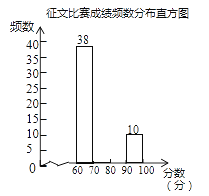
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
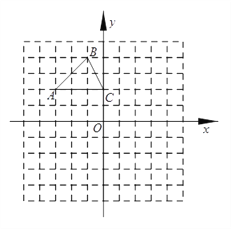
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
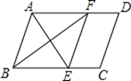
A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
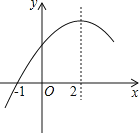
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com