
【题目】等边三角形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向
向![]() 运动,点
运动,点![]() 从
从![]() 出发沿
出发沿![]() 的延长线
的延长线![]() 向右运动,已知点
向右运动,已知点![]() 都以每秒
都以每秒![]() 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中![]() 与
与![]() 相交于点
相交于点![]() .
.
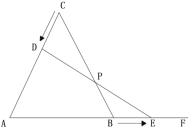
(1)运动几秒后,![]() 为直角三角形?
为直角三角形?
(2)求证:在运动过程中,点![]() 始终为线段
始终为线段![]() 的中点.
的中点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)设x秒时,△ADE为直角三角形,则CD=0.5x,BE=0.5x,AD=40.5x,AE=4+0.5x,根据30°的直角边=斜边的一般建立方程求出其解即可;
(2)作DG∥AB交BC于点E,证明△DGP≌△EBP,就可以得出PD=PE.
(1)∵△ABC是等边三角形,
∴AB=BC=AC=4cm,∠A=∠ABC=∠C=60°.
设x秒时,△ADE为直角三角形,
∴∠ADE=90°,CD=0.5x,BE=0.5x,AD=40.5x,AE=4+0.5x,
∴∠AED=30°,
∴AE=2AD,
∴4+0.5x=2(40.5x),
∴x=![]() ;
;
答:运动![]() 秒后,△ADE为直角三角形;
秒后,△ADE为直角三角形;
(2)作DG∥AB交BC于点G,
∴∠GDP=∠BEP,∠DGP=∠EBP,∠CDG=∠A=60°,∠CGD=∠ABC=60°,
∴∠C=∠CDG=∠CGD,
∴△CDG是等边三角形,
∴DG=DC,
∵DC=BE,
∴DG=BE.
在△DGP和△EBP中
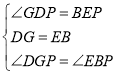 ,
,
∴△DGP≌△EBP(ASA),
∴DP=PE.
∴在运动过程中,点P始终为线段DE的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
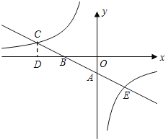
【题目】如图,一次函数![]() 的图象与坐标轴分别交于
的图象与坐标轴分别交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交点为
的图象交点为![]() 、
、![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,若
,若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]()
(1)求一次函数与反比例函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
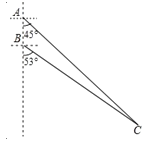
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日为“世界读书日”,每年的这一天,世界100多个国家都会举办各种各样的庆祝和图书宣传活动.我县某书店借此机会决定开展“读书节”活动,为迎接“读书节”制定了活动计划.以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
图书类別 | A类 | B类 |
进价(元/本) | 18 | 12 |
备注 | (1)用不超过16800元购进A、B两类图书共1000本: (2)A类图书不少于600本: | |
(1)陈经理査看计划书时发现:A类图书的标价是B类图书标价的1.5倍,若顾客同样用540元购买图书,能购买A类图书数量比B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现它们高估了“读书节”对图书销售的影响:便调整了销售方案;A类图书每本按标价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
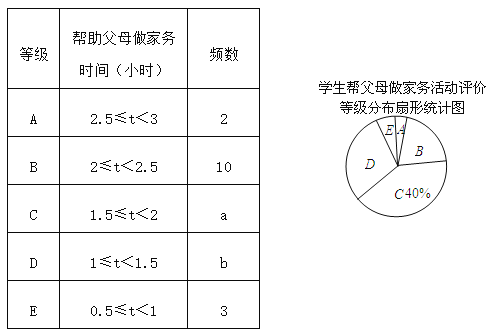
(1)求a,b的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com