
【题目】如图,一次函数![]() 的图象与坐标轴分别交于
的图象与坐标轴分别交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交点为
的图象交点为![]() 、
、![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,若
,若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]()
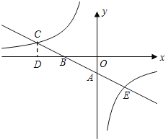
(1)求一次函数与反比例函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的解集.
的解集.
【答案】(1)![]() ,
,![]() ;(2)3;(3)
;(2)3;(3)![]() .
.
【解析】
(1)先利用△AOB的面积为1计算出OA,得到A点坐标,再利用待定系数法求一次函数解析式;接着利用一次函数的解析式确定C点坐标,然后利用待定系数法求反比例函数解析式;
(2))利用反比例函数与一次函数的交点问题解方程组 得E点坐标为(2,-2),然后根据三角形面积公式和S△COE=S△OAC+S△OAE进行计算;
得E点坐标为(2,-2),然后根据三角形面积公式和S△COE=S△OAC+S△OAE进行计算;
(3)观察函数图形得到在y轴左侧,当x<-4时,直线kx+b都在反比例函数y=![]() 的图象上方,从而得到kx+b-
的图象上方,从而得到kx+b-![]() >0的解集.
>0的解集.
解:(1)∵![]() ,
,![]() 的面积为
的面积为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
把![]() 、
、![]() 代入
代入![]() 得
得![]() ,
,
解得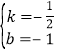 .
.
∴一次函数解析式为![]() ;
;
∵![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴反比例函数解析式为![]() ;
;
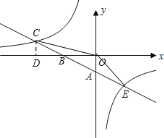
(2)如图,
解方程组 得
得![]() 或
或![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,
![]()
![]()
![]() ;
;
(3)当![]() 时,
时,![]() 的解集为
的解集为![]() .
.
故答案为:(1)![]() ,
,![]() ;(2)3;(3)
;(2)3;(3)![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.
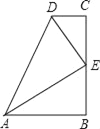
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
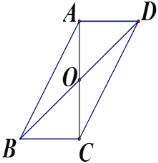
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,若BC=4,AO=CO=3,BD=10,∠ACB=90°,求AD的长及四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,从2018年1月1日起调整居民用水价格,每立方米水费比2017年上涨![]() .小明家2017年8月的水费是18元,而2018年8月的水费是33元.已知小明家2018年8月的用水量比2017年8月的用水量多5 m3.
.小明家2017年8月的水费是18元,而2018年8月的水费是33元.已知小明家2018年8月的用水量比2017年8月的用水量多5 m3.
(1)求该市2017年居民用水的价格;
(2)小明家2019年8月用水量比2018年8月份用水量多了20%,求小明家2019年8月份的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠DFC的度数可以求出来.”
小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”
小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”
......
老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”
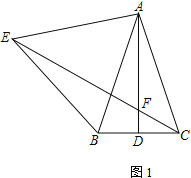
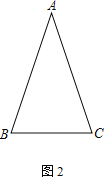
(1)求∠DFC的度数;
(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;
(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
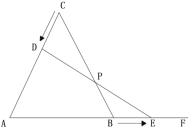
【题目】等边三角形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向
向![]() 运动,点
运动,点![]() 从
从![]() 出发沿
出发沿![]() 的延长线
的延长线![]() 向右运动,已知点
向右运动,已知点![]() 都以每秒
都以每秒![]() 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)运动几秒后,![]() 为直角三角形?
为直角三角形?
(2)求证:在运动过程中,点![]() 始终为线段
始终为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
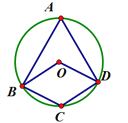
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合)。若四边形OBCD是平行四边形时,那么![]() 的数量关系是________________.
的数量关系是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com