
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠DFC的度数可以求出来.”
小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”
小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”
......
老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”
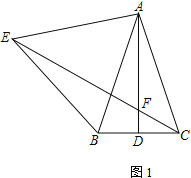
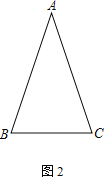
(1)求∠DFC的度数;
(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;
(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.
【答案】(1)60°;(2)EF=AF+FC,证明见解析;(3)AF=EF+2DF,证明见解析.
【解析】
(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;
(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;
(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.
解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,
又△ABE为等边三角形,
∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,
在△ACE中,2α+60°+2β=180°,
∴α+β=60°,
∴∠DFC=α+β=60°;
(2)EF=AF+FC,证明如下:
∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,
∵∠CFD=60°,则∠DCF=30°,
∴CF=2DF,
在EC上截取EG=CF,连接AG,
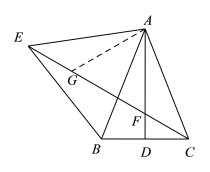
又AE=AC,
∴∠AEG=∠ACF,
∴△AEG≌△ACF(SAS),
∴∠EAG=∠CAF,AG=AF,
又∠CAF=∠BAD,
∴∠EAG=∠BAD,
∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,
∴△AFG为等边三角形,
∴EF=EG+GF=AF+FC,
即EF=AF+FC;
(3)补全图形如图所示,
结论:AF=EF+2DF.证明如下:
同(1)可设∠BAD=∠CAD=α,∠ACE=∠AEC=β,
∴∠CAE=180°-2β,
∴∠BAE=2α+180°-2β=60°,∴β-α=60°,
∴∠AFC=β-α=60°,
又△ABE为等边三角形,∴∠ABE=∠AFC=60°,
∴由8字图可得:∠BAD=∠BEF,
在AF上截取AG=EF,连接BG,BF,
又AB=BE,
∴△ABG≌△EBF(SAS),
∴BG=BF,
又AF垂直平分BC,
∴BF=CF,
∴∠BFA=∠AFC=60°,
∴△BFG为等边三角形,
∴BG=BF,又BC⊥FG,∴FG=BF=2DF,
∴AF=AG+GF=BF+EF=2DF+EF.


科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
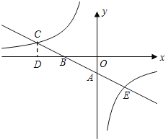
【题目】如图,一次函数![]() 的图象与坐标轴分别交于
的图象与坐标轴分别交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交点为
的图象交点为![]() 、
、![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,若
,若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]()
(1)求一次函数与反比例函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
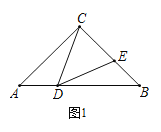
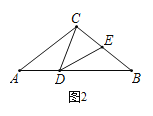
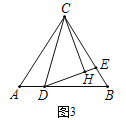
【题目】如图,在等腰△ABC中,AC=BC,D,E分别为AB,BC上一点,∠CDE=∠A.
(1)如图1,若BC=BD,∠ACB=90°,则∠DEC度数为_________°;
(2)如图2,若BC=BD,求证:CD=DE;
(3)如图3,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE-BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
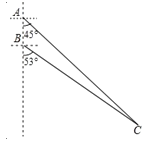
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日为“世界读书日”,每年的这一天,世界100多个国家都会举办各种各样的庆祝和图书宣传活动.我县某书店借此机会决定开展“读书节”活动,为迎接“读书节”制定了活动计划.以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
图书类別 | A类 | B类 |
进价(元/本) | 18 | 12 |
备注 | (1)用不超过16800元购进A、B两类图书共1000本: (2)A类图书不少于600本: | |
(1)陈经理査看计划书时发现:A类图书的标价是B类图书标价的1.5倍,若顾客同样用540元购买图书,能购买A类图书数量比B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现它们高估了“读书节”对图书销售的影响:便调整了销售方案;A类图书每本按标价降低2元销售,B类图书价格不变,那么该书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
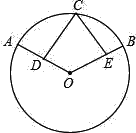
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com