
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:

请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
科目:初中数学 来源: 题型:
【题目】关于反比例函数y= ![]() 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.图象经过点(1,1)
B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称
D.当x<0时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB_____.
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD_____.
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:_____.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年全国两会于3月5日至20日在北京召开,为了了解市民“获取两会新闻的最主要途径”,记者小李开展了一次抽样调查,根据调查结果绘制了如图所示尚不完整的统计图.根据图中信息解答下列问题:

(1)这次接受调查的市民总人数是 ;
(2)扇形统计图中,“电视”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有700万人,请你估计其中将“电脑上网和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 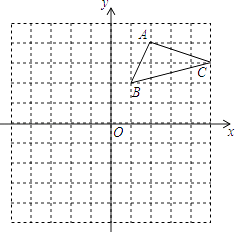
(1)画出△ABC关于x轴对称的△A1B1C1 .
(2)画出△ABC绕原点O旋转180°后的△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2). 
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com