练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．小红和小丽以大树为起点，小红向东走10米记作+10米，小丽向西走8米记作-8米，小红和小丽相距（　　）米．
    A．8米B．10米C．18米D．无法确定

    分析 向东与向西是两个具有相反意义的量，如果向东记作“+”，那么向西就记作“-”，小红向东了10米，表示他离开原地（大树）向东走了10m，小丽向西走了8m，表示它离开原地（大树）向西走了8m，由于东西方向相反，把她们二人走的距离相加即为两人的距离．

    解答 解：小红向东走了10m，记作：+10m，小丽向西走了8m，记作-8m，
    则小红和小丽相距10+8=18（米）；
    故选C．

    点评 本题是考查正、负数的意义及其应用．正、负号表示走的方向，数值表示走的距离．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

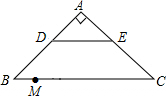    2．如图，在等腰直角三角形ABC中，AB=AC，斜边BC=20，点D，E分别是AB，AC的中点，M是BC上一点，BM=3，点N是线段MC上的一个动点，DN与ME相交于点O，若△OMN是直角三角形，则MN的长是2或$\frac{49}{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知：关于x、y的方程组$\left\{\begin{array}{l}{x+a=6}\\{y-3=a}\end{array}\right.$，则x+y=9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，∠1=∠2，下列选项中不能证明△ABC∽△ADE的是（　　）
    A．∠B=∠DB．∠C=∠EC．$\frac{AD}{AB}$=$\frac{AE}{AC}$D．$\frac{AD}{AB}$=$\frac{DE}{BC}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

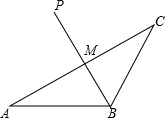    7．图中，△ABC为一钝角三角形，P为△ABC的外心，PB与AC相交于M．
    （1）求证：△ABC为Y一等腰三角形；
    （2）若Q为△ABC的内心，则P、Q及B是否共线？试解释你的答案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列计算正确的是（　　）
    A．2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$B．5$\sqrt{5}$-2$\sqrt{3}$=3$\sqrt{2}$C．$\sqrt{3}$÷$\sqrt{2}$=$\frac{\sqrt{6}}{2}$D．（$\sqrt{5}$）-2=$\frac{2}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知实数x，y满足|x-5|+$\sqrt{y-10}$=0，则以x，y的值为两边长的等腰三角形的周长为（　　）
    A．20或25B．25C．20D．以上答案都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．将一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②中阴影部分的面积（用a、b的代数式表示）是（　　）
    A．a2-b2B．abC．$\frac{a-b}{4}$D．（a-b）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

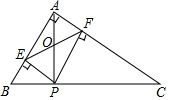    2．如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P是斜边BC上一动点，PE⊥AB于E，PF⊥AC于F，EF与AP相交于点O，则OF的最小值为（　　）
    A．4.8B．1.2C．3.6D．2.4

    查看答案和解析>>

    同步练习册答案