
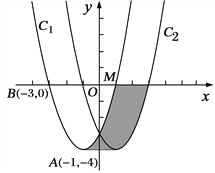
【题目】如图,在平面直角坐标xOy中,抛物线![]() 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)
(1)将抛物线![]() 向右平移2个单位得抛物线
向右平移2个单位得抛物线![]() ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
(2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积![]() =_____________.
=_____________.
【答案】(1)a,b,c的值分别为1,-2,-3;(2)x<-2或x>4;(3)8.
【解析】(1)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,再由平移的规律得出C2的解析式,从而得出a,b,c的值;
(2)令y=5,得出x的值,根据图象得出ax2+bx+c>5的解集.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
(1)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4,
∴a,b,c的值分别为1,-2,-3;
(2)令y=(x-1)2-4中y=5,得x=4或-2.
∴x<-2或x>4时,ax2+bx+c>5,
即ax2+bx+c>5的解集为x<-2或x>4;
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8,


科目:初中数学 来源: 题型:
【题目】阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
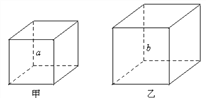
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比(a∶b).
设S甲、S乙分别表示这两个正方体的表面积,则![]()
又设V甲、V乙分别表示这两个正方体的体积,则![]()
(1)下列几何体中,一定属于相似体的是( )
A.两个球体 B.两个锥体 C.两个圆柱体 D.两个长方体
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长的比等于__ __;
②相似体表面积的比等于___ _;
③相似体体积比等于__ __.
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为1.2米,体重为19千克,到了初三时,身高为1.70米,问他的体重是多少?(不考虑不同时期人体平均密度的变化,保留4个有效数学)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与x轴交于(
的图象与x轴交于(![]() , 0)和(
, 0)和(![]() , 0), 其中
, 0), 其中![]() ,与
,与![]() 轴交于正半轴上一点.下列结论:①
轴交于正半轴上一点.下列结论:①![]() ;②
;②![]() ;③a>b;④
;③a>b;④![]() .其中正确结论的序号是____________.
.其中正确结论的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
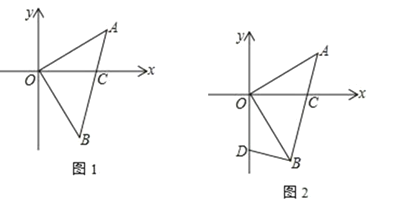
【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
(1) 求△AOB的面积
(2) 如图2,点 D(0,![]() )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com