【题目】在平面直角坐标系
中，点
，将点
向右平移6个单位长度，得到点
．
（1）直接写出点的坐标；
（2）若抛物线
经过点，求
的值；
（3）若抛物线
与线段
有且只有一个公共点时，求抛物线顶点横坐标的取值范围．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B＝2∠C，以点A为圆心，AB长为半径作弧，交BC于点D，交AC于点G；再分别以点B和点D为圆心，大于
BD的长为半径作弧，两弧相交于点E，作射线AE交BC于点F，若以点G为圆心，GC长为半径作两段弧，一段弧过点C，而另一段弧恰好经过点D，则此时∠FAC的度数为（ ）
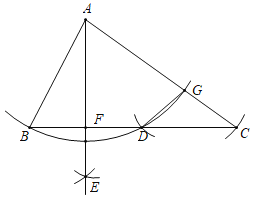
A.54°B.60°C.66°D.72°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠C＝90°，BC＝3，AC＝4，BD平分∠ABC，将△ABC绕着点A旋转后，点B、C的对应点分别记为B1、C1，如果点B1落在射线BD上，那么CC1的长度为_____．
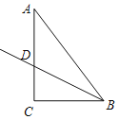
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校准备租用一批汽车，现有甲、乙两种大客车，甲种客车每辆载客量45人，乙种客车每辆载客量30人，已知1辆甲种客车和3辆乙种客车共需租金1240元，3辆甲种客车和2辆乙种客车共需租金1760元．
（1）求1辆甲种客车和1辆乙种客车的租金分别是多少元？
（2）学校计划租用甲、乙两种客车共8辆，送330名师生集体外出活动，最节省的租车费用是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，若点
和点
关于
轴对称，点和点
关于直线
对称，则称点是点关于轴，直线的二次对称点．
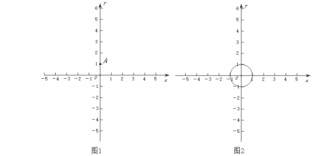
（1）如图1，点
．
①若点
是点
关于轴，直线
：
的二次对称点，则点的坐标为________；
②若点
是点关于轴，直线
:
的二次对称点，则
的值为_______；
③若点
是点关于轴，直线
的二次对称点，则直线的表达式为__________；
（2）如图2，
的半径为1.若上存在点
，使得点
是点关于轴，直绩
:
的二次对称点，且点在射线
上，
的取值范围是________；
（3）
是
轴上的动点，
的半径为2，若上存在点
，使得点
是点关于轴，直线
：
的二次对称点，且点在轴上，求
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线
平行于直线EC，且直线与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线上， 则DF的长为_____
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“长跑”是中考体育考试项目之一．某中学为了解九年级学生“长跑”的情况，随机抽取部分九年级学生，测试其长跑成绩（男子1000米，女子800米），按长跑的时间的长短依次分为A，B，C，D四个等级进行统计，并绘制成如下两幅不完整的统计图．请根据图中提供的信息，解答下列问题：
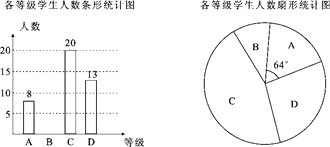
（1）在这次调查中共抽取了 名学生，扇形统计图中，D类所对应的扇形圆心角大小为 ；
（2）所抽取学生“长跑”测试成绩的中位数会落在 等级；
（3）若该校九年级共有900名学生，请你估计该校C等级的学生约在多少人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
