
【题目】操作发现:

(1)数学活动课上,小明将已知△ABO(如图1)绕点O旋转180°得到△CDO(如图2).小明发现线段AB与CD有特殊的关系,请你写出:线段AB与CD的关系是 .
(2)连结AD(如图3),观察图形,试说明AB+AD>2AO.
(3)连结BC(如图4),观察图形,直接写出图中全等的三角形:
(写出三对即可) .
【答案】(1)AB=CD,AB//CD;(2)证明见解析;(3)ΔABO![]() ΔCDO,ΔADO
ΔCDO,ΔADO![]() ΔCBO,ΔABC
ΔCBO,ΔABC![]() ΔCDA,ΔABD
ΔCDA,ΔABD![]() ΔCDB
ΔCDB
【解析】(1)根据图形旋转的性质即可得出结论;
(2)根据三角形三边不等关系得AD+CD>AC,再由旋转的性质得AC=2AO,从而得出结论;
(3)根据三角形全等的判定条件可得出结论.
(1)根据旋转的性质可得:ΔABO![]() ΔCDO,
ΔCDO,
∴AB=CD,∠ABO=∠CDO,
∴AB//CD,
故线段AB与CD的关系是:AB=CD,AB//CD;
(2)在ΔACD中,AD+CD>AC
又因为AB=CD,AO=OC
所以AB+AD>2AO
(3)ΔABO![]() ΔCDO,ΔADO
ΔCDO,ΔADO![]() ΔCBO,ΔABC
ΔCBO,ΔABC![]() ΔCDA,ΔABD
ΔCDA,ΔABD![]() ΔCDB.
ΔCDB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式: ![]() .
.
(2)平方差公式:(a+b)(a-b)= ![]() .
.
(3)常用等价变形: ![]()
![]() ,
,
![]() ,
,
![]() .
.
【题型】单选题
【结束】
10
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
【题目】乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.

![]()
(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
![]() =________;
=________; ![]() =________.
=________.
拓展运用:
(5)计算: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
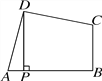
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BD 于点 , 是 AB 上一点,FD 交 AC 于点 E,∠B 与 ∠D 互余.

(1)试说明:∠A=∠D;
(2)若 AE=1,AC=CD=2.5,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1)当x为何值时,OP⊥AP?
(2)求y与x的函数关系式,并写出x的取值范围;
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)若将线段AB绕点O逆时针旋转90°得到线段A1B1,试在图中画出线段A1B1.
(2)若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2.
(3)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com