
【题目】在平面直角坐标系中,正方形![]() 的点
的点![]() ,
,![]() ,
,![]() ,现将此正方形绕
,现将此正方形绕![]() 逆时针旋转
逆时针旋转![]() ,得到正方形
,得到正方形![]() ,求正方形
,求正方形![]() 各顶点的坐标.
各顶点的坐标.
【答案】![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
作A1D⊥x轴于D,C1E⊥x轴于E,如图,根据正方形的性质得OB=2![]() ,∠BOA=∠BOC=45°,再根据旋转的性质得点B1在y轴上,OB1=OB=2
,∠BOA=∠BOC=45°,再根据旋转的性质得点B1在y轴上,OB1=OB=2![]() ,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,则可判断△A1OD和△EOC1都是等腰直角三角形,于是可根据等腰直角三角形的性质得到A1D=OD=
,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,则可判断△A1OD和△EOC1都是等腰直角三角形,于是可根据等腰直角三角形的性质得到A1D=OD=![]() OA1=
OA1=![]() ,C1E=OE=
,C1E=OE=![]() OC1=
OC1=![]() ,然后根据各象限点的坐标特征和y轴上点的坐标特征写出正方形OA1B1C1各顶点的坐标.
,然后根据各象限点的坐标特征和y轴上点的坐标特征写出正方形OA1B1C1各顶点的坐标.
解:作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,如图,
,如图,
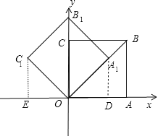
∵正方形![]() 的点
的点![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴正方形![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() ,得到正方形
,得到正方形![]() ,
,
∴点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】(题文)(题文)等边![]() 在平面直角坐标系中,已知点
在平面直角坐标系中,已知点![]() ,将
,将![]() 绕点O顺时针方向旋转
绕点O顺时针方向旋转![]() 得
得![]() .
.
![]() 求出点B的坐标;
求出点B的坐标;
![]() 当
当![]() 与
与![]() 的纵坐标相同时,求出a的值;
的纵坐标相同时,求出a的值;
![]() 在
在![]() 的条件下直接写出点
的条件下直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则DE的长为______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A. 点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动_________秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动_______秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,点D是斜边AB的中点,点E从点B出发以1cm/s的速度向点C运动,点F同时从点C出发以一定的速度沿射线CA方向运动,规定:当点E到终点C时停止运动;设运动的时间为x秒,连接DE、DF.
(1)填空:S△ABC= cm2;
(2)当x=1且点F运动的速度也是1cm/s时,求证:DE=DF;
(3)若动点F以3cm/s的速度沿射线CA方向运动;在点E、点F运动过程中,如果有某个时间x,使得△ADF的面积与△BDE的面积存在两倍关系,请你直接写出时间x的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自![]() 年
年![]() 月
月![]() 日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过
日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元,如果人数超过
元,如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
![]() 如果某单位组织
如果某单位组织![]() 人参加仙都旅游,那么需支付旅行社旅游费用________元;
人参加仙都旅游,那么需支付旅行社旅游费用________元;
![]() 现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用
现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用![]() 元,那么该单位有多少名员工参加旅游?
元,那么该单位有多少名员工参加旅游?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com