【题目】如图，，是一条射线，，一只蚂蚁由以速度向爬行，同时另一只蚂蚁由点以的速度沿方向爬行，几秒钟后，两只蚂蚁与点组成的三角形面积为？

参考答案：

【答案】，，后，两蚂蚁与点组成的三角形的面积均为．

【解析】

设xs后两只蚂蚁与O点组成的三角形面积为450cm2，分当蚂蚁在AO上运动和蚂蚁在OB上运动两种情况列方程，解方程即可求解.

有两种情况：

（1）如图1，当蚂蚁在AO上运动时，设xs后两只蚂蚁与O点组成的三角形面积为450cm2，

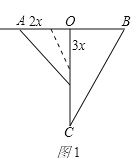
由题意，得×3x×（50-2x）=450，

整理，得x2-25x+150=0，

解得x1=15，x2=10．

（2）如图2，当蚂蚁在OB上运动时，

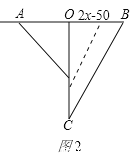
设x秒钟后，两只蚂蚁与O点组成的三角形面积为450cm2，

由题意，得×3x（2x-50）=450，

整理，得x2-25x-150=0，

解得x1=30，x2=-5（舍去）．

答：15s，10s，30s后，两蚂蚁与O点组成的三角形的面积均为450cm2.

关闭