【题目】如图，已知△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，BF、ED的延长线交于点G，连接GC．

（1）求证：AB=GD；

（2）当CG=EG时，且AB=2，求CE．

参考答案：

【答案】（1）见解析；（2）CE=.

【解析】

（1）根据三角形中位线定理得到DE∥AB，AB=2DE，根据平行线的性质得到∠ABF=∠DGF，证明△ABF≌△DGF，根据全等三角形的性质证明结论；

（2）证明△GEC∽△CBA，根据相似三角形的性质列出比例式，计算即可．

解：∵D，E是AC，BC的中点，

∴DE为△ABC的中位线，

∴DE∥AB，AB=2DE，

∴∠ABF=∠DGF，

∵F为AD中点，

∴AF=DF，

在△ABF和△DGF中，

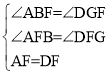
∴△ABF≌△DGF（AAS），

∴AB=GD；

（2）∵AB=2，

∴CD=2，DE=1，

∴GE=3，

∵CA=CB，

∴∠CAB=∠CBA，

∵CG=EG，

∴∠GEC=∠GCE，

∵DE∥AB，

∴∠GEC=∠CBA，

∴△GEC∽△CBA，

设CE=x，

则BC=2x，

∴，即，

解得：，（负值舍去）

∴CE=.

关闭