Question

15．求半径为10cm的圆的内接正十边形的周长（精确到0.01cm）．

Answer 1

分析 设AB是圆内接正十边形的边长，连接OA、OB，作∠OAB的平分线交OB于C，求出∠O=∠CAB，OC=AC=AB，证△OAB∽△ACB，得出比例式，即可求出答案．

解答 解：设AB是圆内接正十边形的边长，连接OA、OB，作∠OAB的平分线交OB于C，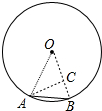
则∠AOB=$\frac{360°}{10}$=36°，
∠OAB=∠OBA=72°，∠OAC=∠BAC=36°，
所以∠ACB=36°+36°=72°，
∵∠B=72°，
∴∠ACB=∠B，
∴AC=AB，AC=OC，
∵∠O=∠CAB=36°，∠B=∠B，
∴△OAB∽△ACB，
∴$\frac{OA}{AB}$=$\frac{AB}{BC}$，即$\frac{10}{AB}$=$\frac{AB}{10-AB}$，
解得，AB=5$\sqrt{5}$-5cm，
则圆的内接正十边形的周长50$\sqrt{5}$-50≈61.80cm．

点评 本题考查了正多边形和圆，等腰三角形的判定，相似三角形的性质和判定的应用，解此题的关键是得出关于AB的比例式，求出边长．