练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

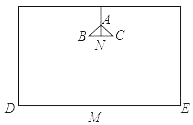
    【题目】在长、宽都为4m，高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡，为了集中光线，加上了灯罩（如图所示）．已知灯罩深AN＝8cm，灯泡离地面2m，为了使光线恰好照在墙角D、E处，灯罩的直径BC应为多少？（结果保留两位小数，≈1.414）

    【答案】灯罩的直径BC约为0. 23m.

    【解析】

    根据题意画出几何图，则AN=0.08m，AM=2m，计算出DE=4m，再证明△ABC∽△ADE，然后利用相似比可计算出BC.

    解：如图，光线恰好照在墙角D. E处，AN=0.08m，AM=2m，

    由于房间的地面是边长为4m的正方形，则DE=4m，

    ∵BC∥DE，

    ∴△ABC∽△ADE，

    ∴，即，

    ∴BC≈0.23(m).

    答：灯罩的直径BC约为0.23m.

    故答案为：约为0.23m.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在中．

    利用尺规作图，在BC边上求作一点P，使得点P到AB的距离的长等于PC的长；

    利用尺规作图，作出中的线段PD．

    要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）

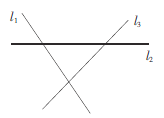
    A.一处B.二处C.三处D.四处

    查看答案和解析>>

    科目：初中数学 来源： 题型：

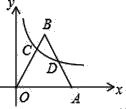
    【题目】如图，在平面直角坐标系中，等边三角形OAB的顶点A的坐标为（5，0），顶点B在第一象限，函数y=（x＞0）的图象分别交边OA、AB于点C、D．若OC=2AD，则k=_____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】圆桌面（桌面中间有一个直径为0.4m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为1.2m，桌面离地面1m，若灯泡离地面3m，则地面圆环形阴影的面积是（ ）

    A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】京沈高速铁路赤峰至喀左段正在建设中，甲、乙两个工程队计划参与一项工程建设，甲队单独施工30天完成该项工程的，这时乙队加入，两队还需同时施工15天，才能完成该项工程．

    （1）若乙队单独施工，需要多少天才能完成该项工程?

    （2）若甲队参与该项工程施工的时间不超过36天，则乙队至少施工多少天才能完成该项工程?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系 xOy 中，抛物线 y = kx 2 - 2k 2 x -3 交 y 轴于 A 点，交直线 x=-4 于 B 点．

    （1）抛物线的对称轴为直线 x=______（用含 k 的代数式表示）；

    （2）若 AB // x 轴，求抛物线的解析式；

    （3）当-4<k<0时，记抛物线在 A，B 之间的部分为图象 G（包含 A，B 两点），若对于图象 G 上任意一点 P（ xP ， yP ）， yP ≥-3 ，结合函数图象写出 k 的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

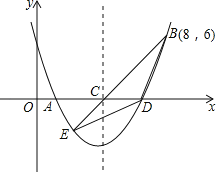
    【题目】如图，二次函数y=x2+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．

    （1）求二次函数的解析式．

    （2）求函数图象的顶点坐标及D点的坐标．

    （3）该二次函数的对称轴交x轴于C点．连接BC，并延长BC交抛物线于E点，连接BD，DE，求△BDE的面积．

    （4）抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S△ADP=S△BCD？若存在，请求出P点的坐标；若不存在．请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学七班共有45人，该班计划为每名学生购买一套学具，超市现有A、B两种品牌学具可供选择已知1套A学具和1套B学具的售价为45元；2套A学具和5套B学具的售价为150元．

    、B两种学具每套的售价分别是多少元？

    现在商店规定，若一次性购买A型学具超过20套，则超出部分按原价的6折出售设购买A型学具a套且不超过30套，购买A、B两种型号的学具共花费w元．

    请写出w与a的函数关系式；

    请帮忙设计最省钱的购买方案，并求出所需费用．

    查看答案和解析>>

    同步练习册答案