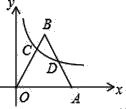
【题目】如图，在平面直角坐标系中，等边三角形OAB的顶点A的坐标为（5，0），顶点B在第一象限，函数y=
（x＞0）的图象分别交边OA、AB于点C、D．若OC=2AD，则k=_____
科目：初中数学 来源： 题型：
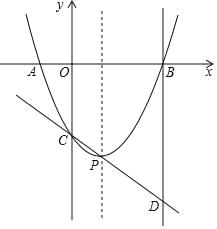
【题目】如图，二次函数 y＝ax2﹣2ax+c(a＞0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点，与 y 轴交于点 C，它的顶点为 P，直线 CP 与过点B 且垂直于 x 轴的直线交于点 D，且 CP：PD＝1：2，tan∠PDB＝
．
(1)则 A、B 两点的坐标分别为 A( ， )； B( ， )；
(2)求这个二次函数的解析式；
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大，则点M 的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
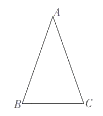
【题目】如图，在△ABC中，AB=AC．
（1）作边AB的垂直平分线MN，交AC于点D，交AB于点E；(保留作图痕迹，不写作法)
（2）连接BD，若AE=5，△CBD的周长为16，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中 5 个黑球， 从袋中随机摸出一球，记下其颜色，这称为依次摸球试验，之后把它放回袋 中，搅匀后，再继续摸出一球．以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表，可以估计出 m 的值是（ ）
A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
科目：初中数学 来源： 题型：
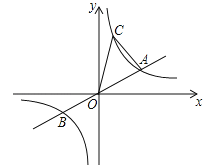
【题目】如图,已知:直线
与双曲线
交于A.B两点，且点A的横坐标为4, 若双曲线
上一点C的纵坐标为8，连接AC.
(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式
的解集.
(3)求三角形AOC的面积
(4) 若在x轴上有点M，y轴上有点N，且点M.N.A.C四点恰好构成平行四边形，直接写出点M.N的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】国庆节期间，南部山区某果园平均每天可卖出 300 斤核桃 ，卖出 1 斤核桃的利润是 1 元，经调查发现，零售单价每降 0.1 元，每天可多卖出 100 斤．设该店决定把零售单价下降 x（0＜x＜1）元．
（1）零售单价下降 x 元后，该店平均每天可卖出多少斤核桃（用 含出 x 的代数式表示，需要简化）；
（2）在不考虑其他国素的条件下，为了薄利多销，当零售单价下降多少时，才能使该店每天获取的利润是 420元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在长、宽都为4m，高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡，为了集中光线，加上了灯罩（如图所示）．已知灯罩深AN＝8cm，灯泡离地面2m，为了使光线恰好照在墙角D、E处，灯罩的直径BC应为多少？（结果保留两位小数，
≈1.414）
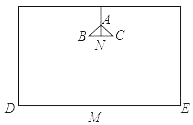
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两名队员参加设计训练，成绩分别被制成下列两个统计图：
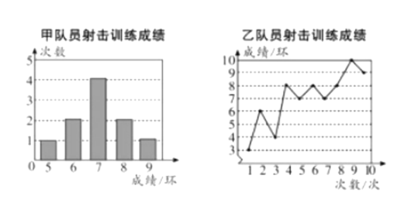
根据以上信息，整理分析数据如下：
平均数（环） | 中位数（环） | 众数（环） | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
（1）表格中
，
，
；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩，若选派其中一名参赛，你认为应选哪名队员？
（3）如果乙再射击
次，命中
环，那么乙的射击成绩的方差 ．（填“变大”“变小”或“不变”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，面积为16的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=1，则小正方形的周长为（ ）
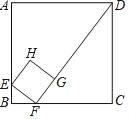
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
