
【题目】如图,面积为16的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=1,则小正方形的周长为( )
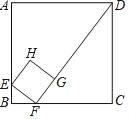
A. 7 B. 6 C. 5 D. 4
科目:初中数学 来源: 题型:
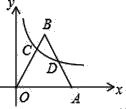
【题目】如图,在平面直角坐标系中,等边三角形OAB的顶点A的坐标为(5,0),顶点B在第一象限,函数y=![]() (x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
(x>0)的图象分别交边OA、AB于点C、D.若OC=2AD,则k=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
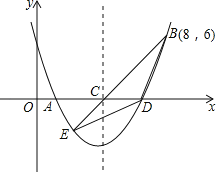
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题发现
如图,![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 经过点
经过点![]() ,与
,与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.

求证:![]() 的周长等于
的周长等于![]() .
.
(1)小明做完该题后,发现![]() 、
、![]() 、
、![]() 存在特定的数量关系,请你直接写出这个数量关系;
存在特定的数量关系,请你直接写出这个数量关系;
拓广探索
(2)如图1,将题中“![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角
的外角![]() ”,其他条件不变,请判断
”,其他条件不变,请判断![]() 、
、![]() 、
、![]() 的数量关系,并证明这个数量关系;
的数量关系,并证明这个数量关系;

(3)如图2,将题中“![]() 平分
平分![]() ,
,![]() 平分
平分![]() ”改为“
”改为“![]() 平分
平分![]() 的外角,
的外角,![]() 平分
平分![]() 的外角”,其他条件不变,请直接写出
的外角”,其他条件不变,请直接写出![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第20届世界杯足球赛正在如火如荼的进行,爸爸想通过一个游戏决定小明能否看今晚的比赛:在一个不透明的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3,![]() , 2
, 2![]() (每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(每张卡片除了上面的实数不同以外其余均相同),爸爸让小明从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小明看比赛,否则就不能看.
(1)请你直接写出按照爸爸的规则小明能看比赛的概率;
(2)小明想了想,和爸爸重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己就看比赛,否则就不看.请你用列表法或树状图法求出按照此规则小明看比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七![]() 班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择
班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择![]() 已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
![]() 、B两种学具每套的售价分别是多少元?
、B两种学具每套的售价分别是多少元?
![]() 现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售
现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售![]() 设购买A型学具a套
设购买A型学具a套![]() 且不超过30套,购买A、B两种型号的学具共花费w元.
且不超过30套,购买A、B两种型号的学具共花费w元.
![]() 请写出w与a的函数关系式;
请写出w与a的函数关系式;
![]() 请帮忙设计最省钱的购买方案,并求出所需费用.
请帮忙设计最省钱的购买方案,并求出所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积;
(3)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com