
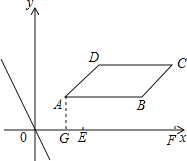
【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.
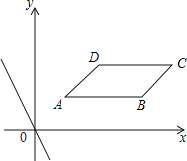
(1)k= ;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)-2;(2)y=﹣2x+6;(3)3≤b≤12;(4)(![]() ,0)或(2
,0)或(2![]() +1,0)或(4﹣2
+1,0)或(4﹣2![]() ,0)
,0)
【解析】
试题分析:(1)根据平行的条件,一次项系数相同,据此即可求得;
(2)设直线l的解析式是y=﹣2x+b,把D的坐标代入解析式即可求得b的值,即可得到函数的解析式;
(3)求得经过A和C的解析式,即可求得;
(4)分成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解.
解:(1)k=﹣2;
(2)设直线l的解析式是y=﹣2x+b,
把(2,2)代入得:﹣4+b=2,解得:b=6,
则直线l的解析式是y=﹣2x+6;
(3)设过A直线l的解析式是y=﹣2x+b,把(1,1)代入得:﹣2+c=1,解得:c=3,
则直线的解析式是y=﹣2x+3,
同理,过C直线l的解析式是y=﹣2x+12,
则3≤b≤12;
(4)当直线l经过A时,解析式是y=﹣2x+3,令y=0,解得x=![]() ,即与x轴的交点是E(
,即与x轴的交点是E(![]() ,0);
,0);
当直线l经过C时,解析式是y=﹣2x+12,令y=0,解得x=6,即与x轴的交点是F(6,0);
当PA=PB时,P在AB的中垂线上,则P的坐标是(![]() ,0);
,0);
当AP=AB=3时,则PG=![]() =2
=2![]() ,则P的坐标是(2
,则P的坐标是(2![]() +1,0);
+1,0);
同理,当BP=BA=3时,P的坐标是(4﹣2![]() ,0).
,0).
故P的坐标是:(![]() ,0)或(2
,0)或(2![]() +1,0)或(4﹣2
+1,0)或(4﹣2![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果抛物线y=3x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系中抛物线的解析式是( )
A. y=3(x﹣2)2+2 B. y=3(x+2)2﹣2
C. y=3(x﹣2)2+2 D. y=3(x+2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知1号、4号两个正方形的面积和为10,2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )
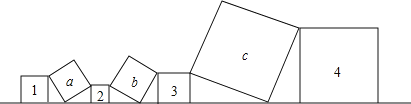
A.17 B.27 C.24 D.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y1=a(x﹣2)2的图象与直线交于A(0,﹣1),B(2,0)两点.
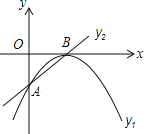
(1)确定二次函数的解析式;
(2)设直线AB解析式为y2,根据图形,确定当y1>y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
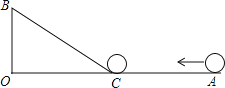
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次考试中,甲,乙两班学生的数据成绩统计如下:
请根据表格提供的信息回答下列问题:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
(1)甲班众数为 分,乙班众数为 分,从众数看成绩较好的是 班;
(2)甲班的中位数是 分,乙班的中位数是 分;
(3)若成绩在80分以上为优秀,则成绩较好的是 班;
(4)甲班的平均成绩是 分,乙班的平均成绩是 分,从平均分看成绩较好的是 班.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com