
��ͼ����ƽ��ֱ������ϵ �У�ֱ��
�У�ֱ��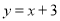 ��x����A�㣬��y����B�㣬��A��B�����������
��x����A�㣬��y����B�㣬��A��B����������� ��
�� ������һ��C����D�������ߵĶ���.
������һ��C����D�������ߵĶ���.

��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ�㣬�������A��B�غϣ�������P�� ��Ĵ��߽�
��Ĵ��߽� ���ڵ�H����ֱ��AB�ڵ�F����PG��AB�ڵ�G������PFG���ܳ������P�������
���ڵ�H����ֱ��AB�ڵ�F����PG��AB�ڵ�G������PFG���ܳ������P�������
��3���������� ���Ƿ���ڳ���D����ĵ�M��ʹ�á�ABM���ABD�������ȣ� �����ڣ��������ʱ��M�����꣬�������ڣ���˵�����ɣ�
���Ƿ���ڳ���D����ĵ�M��ʹ�á�ABM���ABD�������ȣ� �����ڣ��������ʱ��M�����꣬�������ڣ���˵�����ɣ� 
��1�� ����2��P��
����2��P�� ��
�� ������3��M1����2��3����M2��
������3��M1����2��3����M2�� ��
�� ����M3��
����M3�� ��
�� ����
����
��������
�����������1������֪������������κ����Ľ���ʽ���ô���ϵ����ȷ�����κ����Ľ���ʽ���ɣ�
��2�����ȸ��ݡ�PFG�ǵ���ֱ�������Σ���P�� ��
�� ���õ�F��
���õ�F�� ��
�� ���������õ�PF=
���������õ�PF=
 ���Ӷ��õ���PFG�ܳ�Ϊ��
���Ӷ��õ���PFG�ܳ�Ϊ�� ���䷽��ȷ����P�����ꣻ
���䷽��ȷ����P�����ꣻ
��3����DM1��AB��M3M2��AB������AB�������ʱ������ͬ�ȸ߿���ȷ����ABM���ABD�������ȣ��ֱ����ֱ��DM1����ʽΪ�� ��ֱ��M3M2����ʽΪ��
��ֱ��M3M2����ʽΪ�� ������֮����ý������꼴�ɣ�
������֮����ý������꼴�ɣ�
�����������1����ֱ��AB�� �������ύ��A����3��0����B��0��3����
�������ύ��A����3��0����B��0��3����
���������߽���ʽ �У��ã�
�У��ã� ����ã�
����ã� ��
��
�������߽���ʽΪ�� ��
��
��2�����������֪��PFG�ǵ���ֱ�������Σ���P�� ��
�� ������F��
������F�� ��
�� ����
����
��PF=
 ��
��
��PFG�ܳ�Ϊ�� =
= ��
��
�൱ ʱ����PFG�ܳ������ֵ������
ʱ����PFG�ܳ������ֵ������ ʱ��
ʱ�� ����P��
����P�� ��
�� ����
����
��3����M������λ�ã���ͼ��ʾ��M1��M2��M3������ʹ��ABM��������ڡ�ABD�������
��ʱDM1��AB��M3M2��AB������AB������ȣ�
��D����1��4������E����1��2������N����1��0��
�� �У�k=1����ֱ��DM1����ʽΪ��
�У�k=1����ֱ��DM1����ʽΪ�� ��ֱ��M3M2����ʽΪ��
��ֱ��M3M2����ʽΪ�� ��
��
�� ��
�� ��
��
�� ��
�� ��
�� ��
�� ��
��
��M1����2��3����M2�� ��
�� ����M3��
����M3�� ��
�� ����
����

���㣺���κ����ۺ��⣮


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
���䷽����һԪ���η��� ���̿ɻ�Ϊ �� ��
���̿ɻ�Ϊ �� ��
A�� B��
B��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������е���У���꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ�ѡ����
����������⣺
��1����ֱ�������ε������߳�Ϊ5��12��������߳���13��
��2�����a��0����ô ��
��
��3������P �ڵ������ޣ���P��ԭ��˳ʱ����ת90º��P
�ڵ������ޣ���P��ԭ��˳ʱ����ת90º��P
 ��
��
��4���Խ����ഹֱ����ȵ��ı����������Σ�
��5��ijУ������2����7��ͬѧ�����ܲ��Գɼ�����λ���֣����£�50��48��47��50��48��49��48���������ݵ���λ���������Ƿֱ�48��50��
���в���ȷ����ĸ����ǣ� ��
A��4 B��3 C��2 D��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������е���У���꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ�� ������
������ �Ƿ���
�Ƿ��� �Ľ⣮
�Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������ɳƺ�������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��AB/��CD����C��800����CAD��600�����BAD�Ķ������ڣ� ��
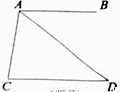
A��500 B��600 C��700 D��400
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������ɳƺ�������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
���� �ĸ��� ��
�ĸ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������У���꼶12���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��ʾ�������߶Ρ����ߺ�ֱ�ߵ�����������˵����ȷ���ǣ� ��

A�������߶Σ���������
B��һ��ֱ�ߣ������߶�
C�������߶Σ��������ߣ�һ��ֱ��
D�������߶Σ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������У���꼶12���¿���ѧ�Ծ��������棩 ���ͣ������
�� ����
���� ��____________��
��____________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com