
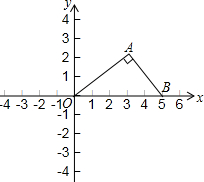 如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.
如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.分析 (1)由题意可得,点B(5,0),点A横坐标与点B横坐标的比为16:25,设点A的坐标为(x,y),列方程得到x=3.2,然后根据勾股定理即可得到结论;
(2)根据三角形的面积公式即可得到结果;
(3)根据已知条件列方程即可得到结论.
解答 解:(1)由题意可得,点B(5,0),点A横坐标与点B横坐标的比为16:25,
设点A的坐标为(x,y)
则,$\frac{x}{5}=\frac{16}{25}$
解得,x=3.2
∵OA=4
∴$y=\sqrt{O{A}^{2}-{x}^{2}}=\sqrt{{4}^{2}-3.{2}^{2}}$=2.4
故点A的坐标为(3.2,2.4)
(2)∵PQ=5-t-3t,
∴S△APQ=$\frac{1}{2}×(5-4t)$×2.4=-$\frac{24}{5}$t+6;
(3)∵S△ABO=$\frac{1}{2}×5×\frac{12}{5}$=6,S△APQ=$\frac{1}{2}$S△ABC,
∴-$\frac{24}{5}$t+6=$\frac{1}{2}×6$,
解得:t=$\frac{5}{8}$;
∴P($\frac{5}{8}$,0),Q($\frac{25}{8}$,0).
点评 本题考查了坐标与图形的性质,三角形的面积,勾股定理,求点的坐标,熟练掌握各知识点是解题的关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
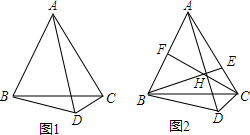
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}=-5$ | B. | 4$\sqrt{3}$-$\sqrt{27}$=1 | C. | $\sqrt{18}÷\sqrt{2}$=9 | D. | $\sqrt{24}•\sqrt{\frac{3}{2}}=6$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
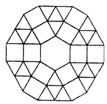 某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)
某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.) 查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:填空题
已知等腰三角形的周长为15若底边长为y cm,一腰长为x cm,则 y与x之间的函数关系式为_____________,自变量x的取值范围是____________
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:单选题
如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为( )

A.  B.
B. 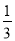 C.
C. 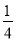 D.
D. 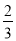
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com