
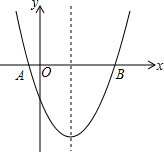
 ��ͼ����֪������y=x2-3x-$\frac{7}{4}$��x�ύ��A��B���㣮
��ͼ����֪������y=x2-3x-$\frac{7}{4}$��x�ύ��A��B���㣮���� ��1����y=0���x��ֵ���ɵó�AB��������꣬���������ߵĶԳ��ṫʽ���ɵó���Գ��᷽�̣�
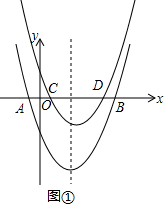
��2���ɣ�1��֪��AB=4������CD��AB=3��4���CD�ij�������y=x2-3x-$\frac{7}{4}$����ƽ��m����λ�ɵó�C��0��0����D��3��0���������ó����ۣ�
��3������ֱ��y=2x+b��b��0���� x��y��ֱ��ڵ�E��F�ó�E��-$\frac{b}{2}$��0����F��0��b������OE=-$\frac{b}{2}$��OF=-b��$\frac{OE}{OF}$=$\frac{1}{2}$���ٷ֡�PFE=90�����PEF=90����������������ۣ�
���  �⣺��1����������y=x2-3x-$\frac{7}{4}$��x�ύ��A��B���㣮
�⣺��1����������y=x2-3x-$\frac{7}{4}$��x�ύ��A��B���㣮
��0=x2-3x-$\frac{7}{4}$�����x1=-$\frac{1}{2}$��x2=$\frac{7}{2}$��
��A��-$\frac{1}{2}$��0����B��$\frac{7}{2}$��0����
�������ߵĶԳ�����x=$\frac{-\frac{1}{2}+\frac{7}{2}}{2}$=$\frac{3}{2}$��
�ʴ�Ϊ����-$\frac{1}{2}$��0������$\frac{7}{2}$��0����$\frac{3}{2}$��
��2����ͼ�٣��ɣ�1��֪��AB=4��
��CD��AB=3��4��
��CD=3��
��y=x2-3x-$\frac{7}{4}$����ƽ��m����λ��
��C��0��0����D��3��0����
��y=x2-3x��
��m=$\frac{7}{4}$��
��3����ֱ��y=2x+b��b��0���� x��y��ֱ��ڵ�E��F��
��E��-$\frac{b}{2}$��0����F��0��b����
��OE=-$\frac{b}{2}$��OF=-b��
��$\frac{OE}{OF}$=$\frac{1}{2}$��
�ٵ���PFE=90��ʱ����ͼ�ڣ���EM��x�ᣬ��PF��M����GM��y����G�����ı���MGOE�Ǿ��Σ�
��MG=OE��EM=OG��
�ߡ�EFO+��MFG=90�㣬��EFO+��FEO=90�㣬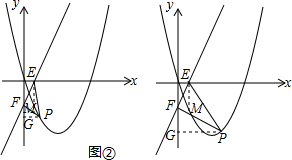
���MFG=��FEO��
�ߡ�EOF=��MGF=90�㣬
���EOF�ס�FGM��
��$\frac{OE}{OF}$=$\frac{FG}{MG}$=$\frac{1}{2}$��
��MG=-$\frac{b}{2}$��
��FG=-$\frac{b}{4}$��
��OG=-b-$\frac{b}{4}$=-$\frac{5}{4}$b��
��M��-$\frac{1}{2}$b��$\frac{5}{4}$b����
�߰�x=-$\frac{1}{2}$b����y=x2-3x����y=$\frac{5}{4}$b��
��M���������ϣ�
��M��ΪP1�㣬
��P��x��x2-3x����
��$\frac{{x}^{2}-3x}{x}$=-$\frac{5}{2}$��
���x1=0����ȥ����x2=$\frac{1}{2}$��
��P1��$\frac{1}{2}$��-$\frac{5}{4}$����
��E��$\frac{1}{2}$��0����F��0��-1����
��ֱ��P1F�Ľ���ʽΪy=-$\frac{1}{2}$x-1��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x-1}\\{y={x}^{2}-3x}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{5}{4}}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$��
��P��$\frac{1}{2}$��-$\frac{5}{4}$����2��-2����
�ڵ���PEF=90��ʱ��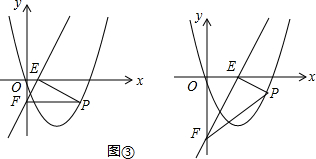
��PE��EF��
����ֱ��PE�Ľ���ʽΪy=-$\frac{1}{2}$x+n��
��E��$\frac{1}{2}$��0����
��0=-$\frac{1}{2}$��$\frac{1}{2}$+n�����n=$\frac{1}{4}$��
��ֱ��PE�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{1}{4}$��
��P1��$\frac{1}{2}$��-$\frac{5}{4}$����P2��$\frac{11}{4}$��-$\frac{11}{16}$����P3��2��-2����P4��$\frac{13}{5}$��-$\frac{36}{25}$����
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����κ���ͼ���ϵ�������ص㡢���κ���ƽ�Ƶ����ʡ�ֱ�������ε����ʵ�֪ʶ���ڽ��3��ʱҪ���з������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | $\frac{1}{4}$ | C�� | -4 | D�� | -$\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
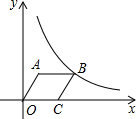 ��ͼ������OABC�Ķ���A������Ϊ��3��4��������C��x����������ϣ�����������y=$\frac{k}{x}$��x��0����ͼ������B�����������ı���ʽΪy=$\frac{32}{x}$��x��0����
��ͼ������OABC�Ķ���A������Ϊ��3��4��������C��x����������ϣ�����������y=$\frac{k}{x}$��x��0����ͼ������B�����������ı���ʽΪy=$\frac{32}{x}$��x��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3+a3=a6 | B�� | $\sqrt{9}$-$\sqrt{5}$=$\sqrt{4}$ | C�� | $\sqrt{��-3��^{2}}$=3 | D�� | ��a-b��2=a2-b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x}{3}$=$\frac{y}{4}$ | B�� | $\frac{x+4}{4}$=$\frac{y+3}{3}$ | C�� | $\frac{x+y}{4+3}$=$\frac{x}{4}$ | D�� | $\frac{4-x}{x}$=$\frac{3-y}{y}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com