Question

【题目】长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图1，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a-3b|+（a+b-4）=0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN=45°

（1）求a、b的值；

（2）若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

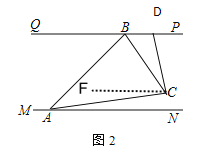
（3）如图2，两灯同时转动，在灯A射线到达AN之前．若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．

Answer 1

【答案】（1）a=3，b=1；（2）A灯转动10秒或85秒时，两灯的光束互相平行；（3）∠BAC与∠BCD的数量关系不发生变化，2∠BAC＝3∠BCD.

【解析】

（1）根据非负数的性质列方程组求解即可；

（2）设A灯转动t秒，两灯的光束互相平行，分两种情况：①在灯A射线到达AN之前；②在灯A射线到达AN之后，分别列出方程求解即可；

（3）设A灯转动时间为t秒，则∠CAN＝180°3t，∠BAC＝∠BAN∠CAN＝3t135°，过点C作CF∥PQ，则CF∥PQ∥MN，得出∠BCA＝∠CBD＋∠CAN＝180°2t，∠BCD＝∠ACD∠BCA＝2t90°，即可得出结果．

解：（1）∵|a-3b|+（a+b-4）=0，

∴，

解得：，

故a=3，b=1；

（2）设A灯转动t秒，两灯的光束互相平行，

①在灯A射线到达AN之前，由题意得：3t＝（20＋t）×1，

解得：t＝10，

②在灯A射线到达AN之后，由题意得：3t180°＝180°（20＋t）×1，

解得：t＝85，

综上所述，A灯转动10秒或85秒时，两灯的光束互相平行；

（3）∠BAC与∠BCD的数量关系不发生变化，2∠BAC＝3∠BCD；

理由：设A灯转动时间为t秒，则∠CAN＝180°3t，

∴∠BAC＝∠BAN∠CAN＝45°（180°3t）＝3t135°，

∵PQ∥MN，

如图2，过点C作CF∥PQ，则CF∥PQ∥MN，

∴∠BCF＝∠CBD，∠ACF＝∠CAN，

∴∠BCA＝∠BCF＋∠ACF＝∠CBD＋∠CAN＝t＋180°3t＝180°2t，

∵CD⊥AC，

∴∠ACD＝90°，

∴∠BCD＝∠ACD∠BCA＝90°（180°2t）＝2t90°，

∴2∠BAC＝3∠BCD.