
【题目】如图,矩形ABCD中,AB=6 cm,BC=8 cm,沿对角线AC将矩形分成两个直角三角形,其中△ABC不动,△A′C′D沿射线CA的方向以每秒2 cm的速度移动.
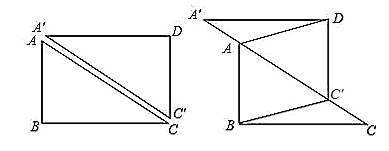
(1)在平移过程中,四边形ABC′D始终是 (请在下面的四个选项中选择一个你认为正确的序号填在横线上);
①平行四边形 ②矩形 ③菱形 ④正方形
(2)在移动过程中,当移动时间t(秒)为何值时,四边形ABC'D是菱形.
【答案】(1)①;(2)当t=![]() 秒时,四边形ABC′D是菱形.
秒时,四边形ABC′D是菱形.
【解析】则(1)直接利用平移的性质得出结论即可判断出四边形ABC'D是平行四边形;
(2)先根据勾股定理求出AC=10,再由菱形的性质得出BD⊥AC',OB=OD,AO=OC'.进而由直角三角形的 面积公式即可求出BO,再根据勾股定理求出AO,最后求出CC'即可求出时间.
(1)由平移得,AB=DC′,AB∥DC′,
∴四边形ABC′D是平行四边形,
故选①;
(2)如图,
,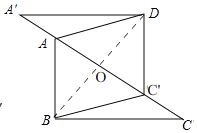
连接BD交AC于点O,
在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵四边形ABC′D是菱形,
∴BD⊥AC′,OB=OD,AO=OC′.
∵12ACBO=12ABBC,
∴BO=ABBCAC=6×810=245,
在Rt△ABO中,AB=6,BO=245,
∴AO=185,
∴C′O=AO=185,
∴AC′=AO+C′O=365,
∴CC′=ACAC′=10365=145,
∴t=145÷2=75,
当t=![]() 秒时,四边形ABC′D是菱形。
秒时,四边形ABC′D是菱形。


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ;点P表示的数是 (用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.

(1)求抛物线的表达式;
(2)在抛物线上是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
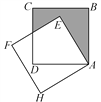
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com