Question

2．将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB=∠DEB=90°，∠A=∠D=30°，点E落在AB上，DE所在直线交AC所在直线于点F．
（1）连接BF，求证：CF=EF．
（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其他条件不变，如图②，求证：AF+EF=DE．
（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其他条件不变，如图③，你认为（2）中的结论还成立吗？若成立，写出证明过程；若不成立，请直接写出AF、EF与DE之间的数量关系．

Answer 1

分析 （1）如图，连接BF，由△ABC≌△DBE，可得BC=BE，根据直角三角形的“HL”判定定理，易证△BCF≌△BEF，即可得出结论；
（2）同（1）得CF=EF，由△ABC≌△DBE，可得AC=DE，AC=AF+CF=AF+EF，即AF+EF=DE；
（3）同（1）得CF=EF，由△ABC≌△DBE，可得AC=DE，AF=AC+FC=DE+EF．

解答 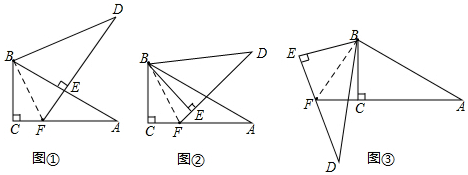（1）证明：如图1，连接BF，
∵△ABC≌△DBE，
∴BC=BE，
∵∠ACB=∠DEB=90°，
在Rt△BCF和Rt△BEF中，
$\left\{\begin{array}{l}{BC=BE}\\{BF=BF}\end{array}\right.$，
∴Rt△BCF≌Rt△BEF（HL），
∴CF=EF；

（2）如图2，连接BF，
∵△ABC≌△DBE，
∴BC=BE，
∵∠ACB=∠DEB=90°，
在Rt△BCF和Rt△BEF中，
$\left\{\begin{array}{l}{BC=BE}\\{BF=BF}\end{array}\right.$，
∴Rt△BCF≌Rt△BEF（HL），
∴EF=CF，
∴AF+EF=AF+CF=AC=DE；

（3）如图3，连接BF，
∵△ABC≌△DBE，
∴BC=BE，
∵∠ACB=∠DEB=90°，
∴△BCF和△BEF是直角三角形，
在Rt△BCF和Rt△BEF中，
$\left\{\begin{array}{l}{BC=BE}\\{BF=BF}\end{array}\right.$，
∴Rt△BCF≌Rt△BEF（HL），
∴CF=EF，
∵AC=DE，
∴AF=AC+FC=DE+EF．

点评 本题主要考查了全等三角形的判定与性质，学生应熟练掌握证明三角形全等的几个判定定理及其性质．解题时注意：全等三角形的对应边相等，对应角相等．