
【题目】某公司投资某个工程项目,现在甲、乙两个工程队有能力承包这个项目.公司调查发现:乙队单独完成工程的时间是甲队的![]() 倍;甲、乙两队合作完成工程需要
倍;甲、乙两队合作完成工程需要![]() 天;甲队每天的工作费用为
天;甲队每天的工作费用为![]() 元、乙队每天的工作费用为
元、乙队每天的工作费用为![]() 元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元?
元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
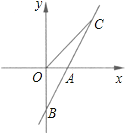
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
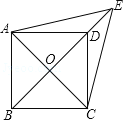
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图:
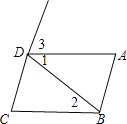
![]() 若
若![]() ,
,
则______ ![]() ______
______ ![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ;
;
若![]() ,
,
则______ ![]() ______
______ ![]() 同旁内角互补,两直线平行
同旁内角互补,两直线平行![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]()
![]() 两直线平行,同位角相等
两直线平行,同位角相等![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]()
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
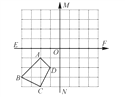
【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com