
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为圆心、2为半径画圆,点
为圆心、2为半径画圆,点![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
(1)当![]() 与
与![]() 相切时,
相切时,
①求证:![]() 是
是![]() 的切线;
的切线;
②求点![]() 到
到![]() 的距离.
的距离.
(2)连接![]() ,
,![]() ,当
,当![]() 的面积最大时,点
的面积最大时,点![]() 到
到![]() 的距离为 .
的距离为 .![]()
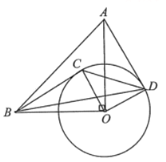
【答案】(1)①见解析,②点C到OB的距离是![]() ;(2)
;(2)![]() .
.
【解析】
(1)①先证明△BOC≌△AOD,则∠BCO=∠ADO=90°,BC是⊙O的切线;
②过点C作CE⊥OB,根据勾股定理得BC=2![]() ,由△BCO的面积公式可得OBCE=BCOC,求得CE=
,由△BCO的面积公式可得OBCE=BCOC,求得CE=![]() ;
;
(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,△BCD的面积最大(如图2),由等腰直角三角形的性质可求得OF=![]() ,则点B到CD的距离为4+
,则点B到CD的距离为4+![]() .
.
(1)①证明:∵AD与⊙O相切,∴∠ADO=90°.
∵∠AOB=∠COD=90°,
∴∠AOB-∠AOC=∠COD-∠AOC,即∠COB=∠AOD,
∵OB=OA,OC=OD,
∴△BOC≌△AOD.
∴∠BCO=∠ADO=90°.
∴BC是⊙O的切线.
②过点C作CE⊥OB,垂足为E,则CE即为点C到OB的距离.
在Rt△BOC中,∵OB=4,OC=2,
∴![]() ,
,
∴OBCE=BCOC,即4CE=2![]() ,CE=
,CE=![]() .
.
∴点C到OB的距离是![]() .
.

(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,
△BCD的面积最大(如图2),此时OB=4,OC=OD=2,
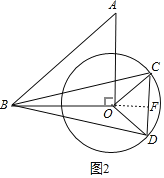
∵△COD是等腰直角三角形,
∴OF=OCsin45°=2×![]() =
=![]() ,
,
∴BF=4+![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
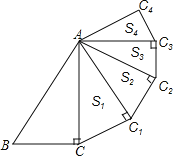
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为斜边作
为斜边作![]() ,使
,使![]() ,
,![]() 的面积记为
的面积记为![]() ,则
,则![]() ______;再以
______;再以![]() 为斜边作
为斜边作![]() ,使
,使![]() ,
,![]() 的面积记为
的面积记为![]() ,……,以此类推,则
,……,以此类推,则![]() ______.(用含
______.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
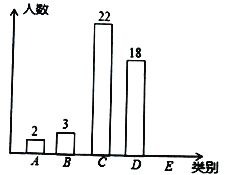
【题目】某班为了解学生每周进行体育锻炼的时间情况,对全班![]() 名学生进行调查,按每周进行体育锻炼的时间
名学生进行调查,按每周进行体育锻炼的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类:![]() 类
类![]() ,
,![]() 类
类![]() ,
,![]() 类
类![]() ,
,![]() 类
类![]() ,
,![]() 类
类![]() .绘制成尚不完整的条形统计图如图. 根据以上信息,解答下列问题:
.绘制成尚不完整的条形统计图如图. 根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班每周进行体育锻炼时间在![]() 的学生中任选人
的学生中任选人![]() 人,求这
人,求这![]() 人每周进行体育锻炼时间都在
人每周进行体育锻炼时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
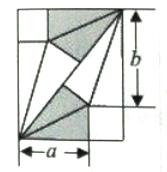
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com