
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC. 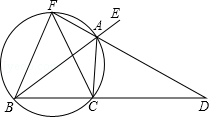
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
【答案】
(1)证明:∵四边形AFBC内接于圆,
∴∠FBC+∠FAC=180°,
∵∠CAD+∠FAC=180°,
∴∠FBC=∠CAD,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAD=∠CAD,
∵∠EAD=∠FAB,
∴∠FAB=∠CAD,
又∵∠FAB=∠FCB,
∴∠FBC=∠FCB;
(2)解:由(1)得:∠FBC=∠FCB,
又∵∠FCB=∠FAB,
∴∠FAB=∠FBC,
∵∠BFA=∠BFD,
∴△AFB∽△BFD,
∴ ![]() ,
,
∴BF2=FAFD=12,
∴BF=2 ![]() ,
,
∵FA=2,
∴FD=6,AD=4,
∵AB为圆的直径,
∴∠BFA=∠BCA=90°,
∴tan∠FBA= ![]() =
= ![]() =
= ![]() ,
,
∴∠FBA=30°,
又∵∠FDB=∠FBA=30°,
∴CD=ADcos30°=4× ![]() =2
=2 ![]() .
.
【解析】(1)由圆内接四边形的性质和邻补角关系证出∠FBC=∠CAD,再由角平分线和对顶角相等得出∠FAB=∠CAD,由圆周角定理得出∠FAB=∠FCB,即可得出结论;(2)由(1)得:∠FBC=∠FCB,由圆周角定理得出∠FAB=∠FBC,由公共角∠BFA=∠BFD,证出△AFB∽△BFD,得出对应边成比例求出BF,得出FD、AD的长,由圆周角定理得出∠BFA=∠BCA=90°,由三角函数求出∠FBA=30°,再由三角函数求出CD的长即可.
【考点精析】根据题目的已知条件,利用三角形的外接圆与外心和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 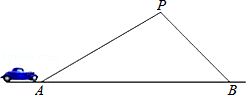
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.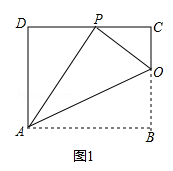
(1)求证:△HCP∽△PDA;
(2)探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
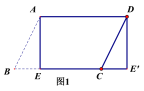
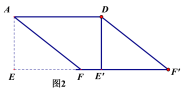
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小青在本学期的数学成绩如下表所示(成绩均取整数):

(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价和零售价(单位:元/kg)如下表所示:
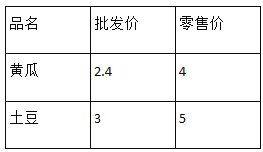
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com