
����Ŀ����ͼ����֪��B��1��3����C��1��0����ֱ��y=x+k������B������x�ύ�ڵ�A������ABC��ֱ��AB�۵��õ���ABD��
��1����գ�A������Ϊ�� �� ����D������Ϊ�� �� ����
��2����������y= ![]() x2+bx+c����C��D���㣬�������ߵĽ���ʽ��
x2+bx+c����C��D���㣬�������ߵĽ���ʽ��
��3������2���е���������y������ƽ�ƣ���ƽ�ƺ�������������y�ύ��ΪE����M��ƽ�ƺ����������ֱ��AB�Ĺ����㣬��������ƽ�ƹ������Ƿ����ijһλ��ʹ��ֱ��EM��x�ᣮ�����ڣ���ʱ����������ƽ���˼�����λ���������ڣ���˵�����ɣ�
����ʾ��������y=ax2+bx+c��a��0���ĶԳ�����x=�� ![]() �����������ǣ���
�����������ǣ��� ![]() ��
�� ![]() ��
��
���𰸡�
��1����2��0����2��3
��2��
�⣺��������y= ![]() x2+bx+c����C��1��0����D����2��3�����룬��ã�b=��
x2+bx+c����C��1��0����D����2��3�����룬��ã�b=�� ![]() ��c=
��c= ![]()
�����������߽���ʽΪ��y= ![]() x2��
x2�� ![]() x+
x+ ![]() ��
��
��3��
�⣺�𣺴��ڣ�
�ߵ���M�������߶Գ���������������ߵĶ���ʱ������M��E�غ�ʱ�����ǵ���������ȣ�
��EM������x��ƽ�У�
����M�������ߵ��Ҳ�ʱ��
������������ƽ��H����λ��ʹEM��x�ᣬ
��ƽ�ƺ�������ߵĽ���ʽΪ
��y= ![]() ��x��1��2+h��
��x��1��2+h��
����������y�ύ��E��0�� ![]() +h����
+h����
�������ߵĶԳ���Ϊ��x=1��
���������ߵĶԳ��ԣ���֪��M������Ϊ��2�� ![]() +h��ʱ��ֱ��EM��x�ᣬ
+h��ʱ��ֱ��EM��x�ᣬ
����2�� ![]() +h������y=x+2��
+h������y=x+2�� ![]() +h=2+2
+h=2+2
��ã�h= ![]() ��
��
������������ƽ�� ![]() ����λ��ʹEM��x�ᣮ
����λ��ʹEM��x�ᣮ
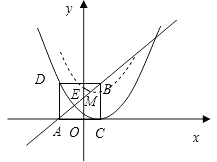
���������⣺��1��A����2��0����D����2��3��
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�ĸ��ֽ��ÿ��С�����εı߳���Ϊ1����С�����εĶ���ΪԲ�ģ�2Ϊ�뾶����һ�����Σ��ø�����Χ��һ��Բ�IJ��棬��Դ�������С����С��ͨ������ó����½��ۣ�С��˵��Բ�IJ����Ϊ ![]() �У�С��˵��Բ�Ļ���Ϊ
�У�С��˵��Բ�Ļ���Ϊ ![]() �У������н�����ȷ���ǣ� ��
�У������н�����ȷ���ǣ� �� 
A.ֻ��С����
B.ֻ��С����
C.���˶���
D.���˶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=24 cm, BC=8 cm����P�ӵ�A��ʼ������A-B-C-D��4 cm/s���ٶ��ƶ�����Q�ӵ�C��ʼ��CD����2 cm/s���ٶ��ƶ��������P��Q�ֱ�ӵ�A��Cͬʱ������������һ�㵽���Dʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊts.��tΪ��ֵʱ���ı���QPBCΪ����?
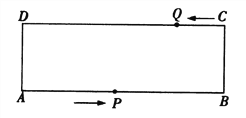
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���|4��1|��ʾ4��1��ľ���ֵ��Ҳ��������Ϊ4��1����������������Ӧ������֮��ľ��룻|4+1|���Կ���|4������1��|����ʾ4�멁1�IJ�ľ���ֵ��Ҳ��������Ϊ4�멁1����������������Ӧ�������ľ��룮
��1��|4������1��|=�� ��
��2��|5+2|=�� ��
![]()
��3�����������ҳ����з�������������x��ʹ��|x+3|=5����x=�� ����
��4�����������ҳ����з�������������x��ʹ��|x+3|+|x��2|=5�������������ǣ��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=65������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����
��1����ͼ�٣������ǰ�MON��һ��ON������OB�غ�ʱ�����MOC=�� ����
��2����ͼ�ڣ������ǰ�MON�Ƶ�O��ʱ����תһ���Ƕȣ���ʱOC�ǡ�MOB�Ľ�ƽ���ߣ�����ת�ǡ�BON=�� ������CON=�� ����
��3�������ǰ�MON�Ƶ�O��ʱ����ת��ͼ��ʱ����NOC=5�������AOM��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С�����εĶ�������������ABC����������A��B��C���ڸ����������ABC�Ƶ�A��˳ʱ�뷽����ת90��õ���AB��C����

��1���������������У�������AB��C�䣻
��2�������߶�AB�ڱ任��AB��Ĺ�����ɨ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼa��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ��ʵ���ü������ֳ��Ŀ�С�����Σ�Ȼ��ͼb����״ƴ��һ�������Σ�

��1��ͼb�У��������εı߳����� ������Ӱ����С�����εı߳����� ����
��2���۲�ͼb��д����m+n��2����m��n��2��mn֮���һ��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ�Ȼ�������⣮
̽�����õ��ݵ���ʽ��ʾaman�Ľ����m��Ϊ����������
���ݳ˷������壬aman=![]() =am+n��
=am+n��
��1����������Ͻ�����գ�36��38=�� ����52��53��57=�� ������a+b��3��a+b��5=�� ����
��2���������ϵķ������̣��õ��ݵ���ʽ��ʾ��am��n�Ľ������ʾ����am����һ�����壩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���߳�Ϊ2����A����C�ֱ���x�ᣬy����������ϣ�����y=2x��ͼ����CB���ڵ�D������y= ![]() ��kΪ������k��0����ͼ����D����AB���ڵ�E���뺯��y=2x��ͼ���ڵ��������ڽ��ڵ�F������AF��EF��
��kΪ������k��0����ͼ����D����AB���ڵ�E���뺯��y=2x��ͼ���ڵ��������ڽ��ڵ�F������AF��EF�� 
��1������y= ![]() �ı���ʽ����ֱ��д��E��F��������ꣻ
�ı���ʽ����ֱ��д��E��F��������ꣻ
��2�����AEF�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com