
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
【答案】
(1)2
(2)解:当O在BC上时,如图(1)所示:连接OD,过点A作AE⊥BC.

∵AB=AC,AE⊥BC,
∴BE=EC=3.
在△AEB中,由勾股定理可知AE= ![]() =4.
=4.
∵AB与⊙O相切,
∴OD⊥AB.
∴∠BDO=∠BEA=90°.
又∵∠OBD=∠EBA,
∴△ODB∽△AEB.
∴ ![]() .
.
设⊙O的半径为r.在OB=6﹣r.
∴ ![]() .
.
∴r= ![]() .
.
∴△ABC的BC边上的伴随圆的半径为 ![]() .
.
当O在AB上时,如图(2),连接OD、过点A作AE⊥BC,垂足为E.

∵BC与⊙O相切,∴OD⊥BC.又∵AE⊥BC,
∴OD∥AE.∴△BOD∽△BAE.
∴ ![]() .
.
设⊙O的半径为r,则OB=5﹣r.∴ ![]() .∴r=
.∴r= ![]() .
.
如图(3)所示:连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.

∵S△ABC= ![]() BCAE=
BCAE= ![]() ACBF,∴
ACBF,∴ ![]() ×6×4=
×6×4= ![]() ×5×BF.∴BF=4.8.
×5×BF.∴BF=4.8.
∵AC与⊙O相切,∴DO⊥AC.∴DO∥BF.
∴△AOD∽△ABF.∴ ![]() 即
即 ![]() .∴r=
.∴r= ![]() .
.
综上所述,△ABC的伴随圆的半径分为 ![]() 或
或 ![]() 或
或 ![]()
(3)解:①证明:如图(4)连接OP、OB.

∵△CPD为直角三角形,
∴△CPD的外接圆圆心O在CD中点.
设⊙O的半径为r,则DC=2r,OA=3r.∴ ![]() .∵PA=2BP,
.∵PA=2BP,
∴ ![]() .∴
.∴ ![]() .∴PD∥OB.∴∠1=∠2,∠3=∠4.
.∴PD∥OB.∴∠1=∠2,∠3=∠4.
又∵∠3=∠2,∴∠1=∠4.在△BCO和△BPO中  ,∴△BCO≌△BPO.
,∴△BCO≌△BPO.
∴∠BPO=∠BCO=90°.∴AB是圆O的切线.
∴△CPD的外接圆是△ABC某一条边上的伴随圆.
②如图(4)设圆O的半径为r.
∵在Rt△OAP中,OA=3r,OP=r,
∴PA= ![]() =2
=2 ![]() r.
r.
∴AB=3 ![]() r.
r.
∵在Rt△ABC中,AC=4r,AB=3 ![]() r,
r,
∴BC= ![]() =
= ![]() a.
a.
∵在Rt△OBC中,OC=r,BC= ![]() r,
r,
∴OB= ![]() =
= ![]() r.
r.
∴cos∠1= ![]() =
= ![]() =
= ![]() .
.
∵∠PDC=∠1,
∴cos∠PDC= ![]()
【解析】(1)∵∠C=90°,AB=5,BC=3,
∴AC= ![]() =4.
=4.
∵BC是圆的切线,∠BCA=90°,
∴AC为圆的直径.
∴AC边上的半随圆的半径为2.
所以答案是:2.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】如图,在第一象限内,点P(2,3),M(a,2)是双曲线y= ![]() (k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 .
(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示. 
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() 满足
满足![]() .
.

(1)填空:![]() _______,
_______,![]() ________;
________;
(2)若在第三象限内有一点![]() ,用含
,用含![]() 的式子表示
的式子表示![]() 的面积;
的面积;
(3)在(2)条件下,当![]() 时,点
时,点![]() 是坐标轴上的动点,当满足
是坐标轴上的动点,当满足![]() 的面积是
的面积是![]() 的面积的2倍时,求点
的面积的2倍时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】
如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①②,![]() 的两边分别平行.
的两边分别平行.
(1)在图①中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(2)在图②中,![]() 与
与![]() 有什么数量关系?为什么?
有什么数量关系?为什么?
(3)由(1)(2)你能得出什么结论?用一句话概括你得到的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A.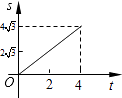
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ![]() ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com