
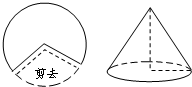
 如图,如果从半径为3的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是$\sqrt{5}$.
如图,如果从半径为3的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是$\sqrt{5}$. 分析 首先求得扇形的圆心角,然后求得扇形的弧长,从而求得底面的半径,利用勾股定理求得圆锥的高即可.
解答 解:∵从半径为3的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,
∴留下的扇形圆心角为:360°×$\frac{2}{3}$=240°,
∴留下的扇形的弧长=$\frac{240π×3}{180}$=4π,
根据底面圆的周长等于扇形弧长,
∴圆锥的底面半径r=$\frac{4π}{2π}$=2,
所以圆锥的高=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题主要考查了圆锥的性质,要知道(1)圆锥的高,底面半径,母线构成直角三角形,(2)此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
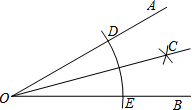 如图,已知∠AOB.小明按如下步骤作图:
如图,已知∠AOB.小明按如下步骤作图:| A. | 射线OC是∠AOB的平分线 | B. | 线段DE平分线段OC | ||
| C. | 点O和点C关于直线DE对称 | D. | OE=CE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中位数 | B. | 平均数 | C. | 最高分数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com