
【题目】已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ=24,则OM的长为 . 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )

A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y=![]() 时,x=10
时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.


图⑴ 图⑵
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”是对古丝绸之路的传承和提升,让中国和世界的联系更紧密,电气设备是“一带一路”沿线国家受青睐的商品。某企业计划生产甲、乙两种电气设备出口,甲种设备售价50千元/件,乙种设备售价30千元/件,生产这两种设备需要A、B两种原料,生产甲设备需要A种原料4吨/件,B种原料2吨/件,生产乙设备需要A种原料3吨/件,B种原料1吨/件,已知A种原料有120吨,B种原料有50吨.
(1)如何安排生产,才能恰好使A、B两种原料全部用完?此时总产值是多少千元?
(2)若使甲种设备售价上涨10%,而乙种设备售价下降10%,并且要求甲种设备比乙种设备多生产25件,问如何安排甲、乙两种设备的生产,使销售总产值能达到1375千元,此时A、B两种原料还剩下多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
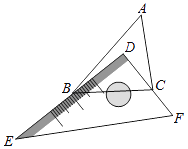
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com