
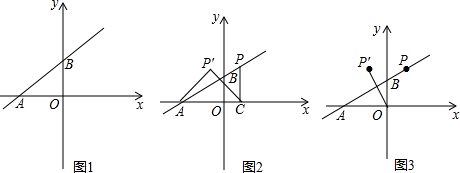
ЗжЮі ЃЈ1ЃЉЂйгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓГівЛДЮКЏЪ§НтЮіЪНЃЛ
ЂкЩшГіQЕузјБъЃЈmЃЌ0ЃЉЃЌгЩШЋЕШПЩЕУГіЙигкmЕФвЛДЮЗНГЬЃЌНтЗНГЬМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнЕуаБЪНаДГіжБЯпABЕФНтЮіЪНЃЌгЩДЫПЩЕУГіPЕуЁЂCЕуКЭPЁфЕуЕФзјБъЃЌгЩЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУГіИїБпЕФЙиЯЕЃЌгЩДЫЕУГіЙигкaЁЂbЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЗНГЬзщМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉНсКЯЃЈ2ЃЉжБЯпЕФНтЮіЪНКЭPЁЂPЁфЕуЕФзјБъЃЌгЩЯпЖЮOPЁфЧЁКУБЛжБЯпABДЙжБЦНЗжПЩЕУжЊOPЁфЕФаБТЪгыABаБТЪЛЅЮЊИКЕЙЪ§ЃЌЧвOPЁфЕФжаЕудкжБЯпABЩЯЃЌгЩДЫПЩЕУГіЙигкaЁЂbЕФЖўдЊЖўДЮЗНГЬзщЃЌНтЗНГЬзщМДПЩЕУГіНсТлЃЎ
НтД№ НтЃКЃЈ1ЃЉЂйЩшжБЯпABЕФКЏЪ§БэДяЪНЮЊy=kx+bЃЌ
ЁпЕуAЕФзјБъЪЧЃЈ-4ЃЌ0ЃЉЃЌЕуBЕФзјБъЪЧЃЈ0ЃЌ3ЃЉ
Ёрга$\left\{\begin{array}{l}{0=-4k+b}\\{3=b}\end{array}\right.$ЃЌНтЕУЃК$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$ЃЎ
ЙЪжБЯпABЕФКЏЪ§БэДяЪНЮЊy=$\frac{3}{4}$x+3ЃЎ
ЂкЁпЕуPЪЧжБЯпABЩЯЕФвЛИіЖЏЕуЃЌЕуQЮЊxжсЩЯвЛЕуЃЈЕуOГ§ЭтЃЉЃЌ
ЁрЩшЕуQЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЁЯPAQ=ЁЯBAOЃЌ
ЁрAQ=|m+4|ЃЎ
дкRtЁїAOBжаЃЌAO=4ЃЌBO=3ЃЌAB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5ЃЎ
ЁїAPQгыЁїAOBШЋЕШгаСНжжЧщПіЃК
ЕБAQ=AOЪБЃЌМД|m+4|=4ЃЌ
НтЕУЃКm=0ЃЈЩсШЅЃЉЃЌЛђm=-8ЃЌ
ДЫЪБЕуQЕФзјБъЮЊЃЈ-8ЃЌ0ЃЉЃЛ
ЕБAQ=ABЪБЃЌМД|m+4|=5ЃЌ
НтЕУЃКm=-9ЃЌЛђm=1ЃЌ
ДЫЪБЕуQЕФзјБъЮЊЃЈ-9ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
злЩЯЫљЪіЃКЕуQЕФЫљгазјБъЮЊЃЈ-9ЃЌ0ЃЉЃЌЃЈ-8ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ-9ЃЌ0ЃЉЃЌЃЈ-8ЃЌ0ЃЉЛђЃЈ1ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЙ§PЁфзїPDЁЭxжсгкЕуDЃЌШчЭМЫљЪОЃЎ
ЁпЕуAЕФзјБъЪЧЃЈ-4ЃЌ0ЃЉЃЌЕуBЕФзјБъЪЧЃЈ0ЃЌbЃЉЃЈbЃО0ЃЉЃЌ
ЁржБЯпABЕФаБТЪЮЊ$\frac{b-0}{0-ЃЈ-4ЃЉ}$=$\frac{b}{4}$ЃЌ
МДжБЯпABЕФНтЮіЪНЮЊy=$\frac{b}{4}$x+bЃЎ
ЁпЕуPдкжБЯпABЩЯЃЌ
ЁрЕуPЕФзјБъЮЊЃЈaЃЌ$\frac{b}{4}$a+bЃЉЃЌдђЕуPЁфЕФзјБъЮЊЃЈ-aЃЌ$\frac{b}{4}$a+bЃЉЃЌЕуCЕФзјБъЮЊЃЈaЃЌ0ЃЉЃЌЕуDЕФзјБъЮЊЃЈ-aЃЌ0ЃЉЃЌ
ЁрPЁфD=$\frac{b}{4}$a+bЃЌAC=a+4ЃЌAD=4-aЃЎ
ЁпЕуPЮЊЕквЛЯѓЯоЕФЕуЃЌ
ЁрaЃО0ЃЎ
ЁпЁїACPЁфЪЧвдЕуPЁфЮЊжБНЧЖЅЕуЕФЕШбќжБНЧШ§НЧаЮЃЌ
Ёрга$\left\{\begin{array}{l}{PЁфD=\frac{1}{2}AC}\\{PЁфD=AD}\end{array}\right.$ЃЌМД$\left\{\begin{array}{l}{\frac{b}{4}a+b=\frac{a+4}{2}}\\{\frac{b}{4}a+b=4-a}\end{array}\right.$ЃЌ
НтЕУЃК$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=2}\end{array}\right.$ЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЃКЕуPЕФзјБъЮЊЃЈaЃЌ$\frac{b}{4}$a+bЃЉЃЌдђЕуPЁфЕФзјБъЮЊЃЈ-aЃЌ$\frac{b}{4}$a+bЃЉЃЌжБЯпABЕФНтЮіЪНЮЊy=$\frac{b}{4}$x+bЃЎ
дђOPЁфЕФжаЕузјБъЮЊЃЈ-$\frac{a}{2}$ЃЌ$\frac{b}{8}a+\frac{b}{2}$ЃЉЃЌжБЯпOPЁфЕФаБТЪЮЊ$\frac{\frac{b}{4}a+b-0}{-a-0}$=-$\frac{b}{4}$-$\frac{b}{a}$ЃЎ
ЁпЯпЖЮOPЁфЧЁКУБЛжБЯпABДЙжБЦНЗжЃЌ
Ёрга$\left\{\begin{array}{l}{\frac{b}{8}a+\frac{b}{2}=\frac{b}{4}ЃЈ-\frac{a}{2}ЃЉ+b}\\{\frac{b}{4}ЃЈ-\frac{b}{4}-\frac{b}{a}ЃЉ=-1}\end{array}\right.$ЃЌ
НтЕУЃК$\left\{\begin{array}{l}{a=2}\\{b=\frac{4\sqrt{3}}{3}}\end{array}\right.$ЃЌЛђ$\left\{\begin{array}{l}{a=2}\\{b=-\frac{4\sqrt{3}}{3}}\end{array}\right.$ЃЈЩсШЅЃЉЃЎ
ЙЪД№АИЮЊЃК$\frac{4\sqrt{3}}{3}$ЃЎ
ЕуЦР БОЬтПМВщСЫД§ЖЈЯЕЪ§ЧѓНтЮіЪНЁЂвЛДЮКЏЪ§ЕФаБТЪЁЂШЋЕШШ§НЧаЮЕФаджЪЁЂСНДЙжБжБЯпМфаБТЪЕФЙиЯЕвдМАНтЖўдЊвЛДЮЃЈЖўДЮЃЉЗНГЬзщЃЌНтЬтЕФЙиМќЃКЃЈ1ЃЉЂйД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЃЛЂкгЩШЋЕШШ§НЧаЮЕФаджЪевГіЙигкmЕФвЛдЊвЛДЮЗНГЬЃЛЃЈ2ЃЉРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪевГіЙигкaЁЂbЕФЖўдЊвЛДЮЗНГЬЃЛЃЈ3ЃЉРћгУДЙжБЦНЗжЯпЕФаджЪЕУГіЙигкaЁЂbЕФЖўдЊЖўДЮЗНГЬзщЃЎБОЬтЪєгкФбЬтЃЌЃЈ1ЃЉФбЖШВЛЪЧКмДѓЃЛЃЈ2ЃЉНшжњБпЕФЙиЯЕМђЛЏСЫЗНГЬзщЃЌШєгУСНЕуМфЕФОрРыЙЋЪННсКЯЙДЙЩЖЈРэСаГіЗНГЬзщКмИДдгЃЌЙЪзіДЫРрЬтФПЪБЃЌФмМђЛЏЗНГЬвЛЖЈвЊМђЛЏЃЛЃЈ3ЃЉЁАСНЬѕжБЯпДЙжБЃЌаБТЪГЫЛ§ЮЊ-1ЃЈгааБТЪЕФЧщПіЯТЃЉЁБЫфЫЕЮЊИпжажЊЪЖЃЌЕЋдкГѕжазіЬтжавЛжБдкдЫгУЃЌРћгУетИіНсТлФмДјРДКмДѓЕФЗНБуЃЌвђДЫдкШеГЃНЬбЇжаРЯЪІУЧЖМФУДЫНсТлЕБаджЪЖЈРэРДгУЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ДЙжБ | BЃЎ | ЦНаа | CЃЎ | жиКЯ | DЃЎ | ЯрНЛ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 8x2y | BЃЎ | -8x6y | CЃЎ | -8x6y3 | DЃЎ | 8x6y3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
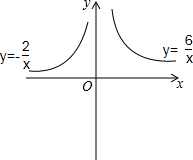 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖЏЕуAДгдЕуOГіЗЂбиyжсе§АыжсвдУПУы1ЕЅЮЛГЄЖШдЫЖЏЃЌдЫЖЏЕФЪБМфЮЊtУыЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌНЛКЏЪ§y=-$\frac{2}{x}$ЃЈxЃМ0ЃЉЕФЭМЯѓгкBЃЌНЛКЏЪ§y=$\frac{6}{x}$ЃЈxЃО0ЃЉЕФЭМЯѓгкCЃЌзїЩфЯпBOЃЌЕуDЪЧЩфЯпBOЩЯвЛИіЖЏЕуЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖЏЕуAДгдЕуOГіЗЂбиyжсе§АыжсвдУПУы1ЕЅЮЛГЄЖШдЫЖЏЃЌдЫЖЏЕФЪБМфЮЊtУыЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌНЛКЏЪ§y=-$\frac{2}{x}$ЃЈxЃМ0ЃЉЕФЭМЯѓгкBЃЌНЛКЏЪ§y=$\frac{6}{x}$ЃЈxЃО0ЃЉЕФЭМЯѓгкCЃЌзїЩфЯпBOЃЌЕуDЪЧЩфЯпBOЩЯвЛИіЖЏЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌжБЯпy1=x+2гыЫЋЧњЯпy2=$\frac{k}{x}$НЛгкAЃЈmЃЌ4ЃЉЃЌBЃЈ-4ЃЌnЃЉЃЎ
ШчЭМЃЌжБЯпy1=x+2гыЫЋЧњЯпy2=$\frac{k}{x}$НЛгкAЃЈmЃЌ4ЃЉЃЌBЃЈ-4ЃЌnЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
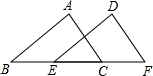 ШчЭМЃЌдкШ§НЧаЮABCжаЃЌBC=8ЃЌНЋШ§НЧаЮABCвдУПУы2cmЕФЫйЖШбиBCЫљдкжБЯпЯђгвЦНвЦЃЌЫљЕУЕФЭМаЮЖдгІЮЊШ§НЧаЮDEFЃЌЩшЦНвЦЕФЪБМфЮЊtУыЃЌЕБt=ЃЈЁЁЁЁЃЉЪБЃЌAD=CEЃЎ
ШчЭМЃЌдкШ§НЧаЮABCжаЃЌBC=8ЃЌНЋШ§НЧаЮABCвдУПУы2cmЕФЫйЖШбиBCЫљдкжБЯпЯђгвЦНвЦЃЌЫљЕУЕФЭМаЮЖдгІЮЊШ§НЧаЮDEFЃЌЩшЦНвЦЕФЪБМфЮЊtУыЃЌЕБt=ЃЈЁЁЁЁЃЉЪБЃЌAD=CEЃЎ| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | 3 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com