
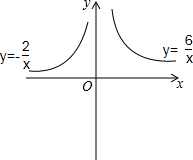
 如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.
如图,在平面直角坐标系中,动点A从原点O出发沿y轴正半轴以每秒1单位长度运动,运动的时间为t秒,过点A作x轴的平行线,交函数y=-$\frac{2}{x}$(x<0)的图象于B,交函数y=$\frac{6}{x}$(x>0)的图象于C,作射线BO,点D是射线BO上一个动点.分析 (1)根据纵坐标求得B、C的横坐标即可求得;
(2)设A的纵坐标为m,则B(-$\frac{2}{m}$,m),C($\frac{6}{m}$,m),证得△EOB∽△FOD,然后根据相似三角形的性质得出DF=3m,进一步求得CD=4m,然后根据三角形面积公式即可求得;
(3)分两种情况分别讨论求得即可.
解答 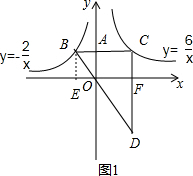 解:(1)当t=$\sqrt{3}$时,B、C的纵坐标为$\sqrt{3}$,
解:(1)当t=$\sqrt{3}$时,B、C的纵坐标为$\sqrt{3}$,
代入y=-$\frac{2}{x}$(x<0)得$\sqrt{3}$=-$\frac{2}{x}$,
解得x=-$\frac{2}{3}$$\sqrt{3}$
代入y=$\frac{6}{x}$(x>0)得,$\sqrt{3}$=$\frac{6}{x}$,
解得x=2$\sqrt{3}$,
∴BC=2$\sqrt{3}$+$\frac{2}{3}$$\sqrt{3}$=$\frac{8}{3}$$\sqrt{3}$;
(2)过B作BE⊥x轴于E,如图1,
∵BC∥x轴,
∴CD⊥x轴,B、C的纵坐标相同,设A的纵坐标为m,则B(-$\frac{2}{m}$,m),C($\frac{6}{m}$,m),
∴BE=m,OE=$\frac{2}{m}$,OF=$\frac{6}{m}$,
∵∠OEB=∠OFD=90°,∠EOB=∠FOD,
∴△EOB∽△FOD,
∴$\frac{DF}{BE}$=$\frac{OF}{OE}$,即$\frac{DF}{m}$=$\frac{\frac{6}{m}}{\frac{2}{m}}$,
∴DF=3m,
∴CD=4m,
∵BC=$\frac{6}{m}$+$\frac{2}{m}$=$\frac{8}{m}$,
∴S△BCD=$\frac{1}{2}$BC•CD=$\frac{1}{2}$×$\frac{8}{m}$×4m=16;
(3)∵CD=4m,BC=$\frac{8}{m}$,
①如图1,当CD=BC时,则4m=$\frac{8}{m}$,
解得m=$\sqrt{2}$,
∴A的纵坐标为$\sqrt{2}$,
∴t=$\sqrt{2}$,
∴D(3$\sqrt{2}$,-3$\sqrt{2}$)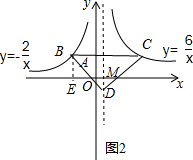
②如图2,当CD=BD时,∵B(-$\frac{2}{m}$,m),C($\frac{6}{m}$,m),
∴D点的横坐标为$\frac{2}{m}$,
设直线OB的解析式为y=kx,
∴m=-$\frac{2}{m}$k,解得k=-$\frac{{m}^{2}}{2}$,
∴直线OB的解析式为y=-$\frac{1}{2}$m2x,
把x=$\frac{2}{m}$代入得y=-$\frac{1}{2}$m2×$\frac{4}{{m}^{2}}$=2,
∵OM=OE=$\frac{2}{m}$,
∴BE=DM=2,
∴A的纵坐标为2,D(1,-2)
∴t=2,
综上,t为$\sqrt{2}$和2时,△BCD为等腰直角三角形,此时D的坐标为(3$\sqrt{2}$,-3$\sqrt{2}$)或(1,-2).
点评 本题是反比例函数的综合题,考查了反比例函数图象上的坐标特征,三角形相似的判定和性质,直角三角形判定和性质等,注意分类讨论思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
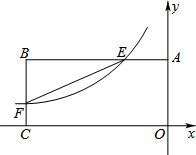 如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).
如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com