
| A. | 垂直 | B. | 平行 | C. | 重合 | D. | 相交 |
分析 作出图形,然后根据两直线平行,同旁内角互补以及角平分线的定义可得∠1+∠2=90°,再根据三角形的内角和定理求出∠C=90°,从而得解.
解答 解:如图,∵a∥b,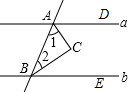
∴∠DAB+∠ABE=180°,
∵AC、BC分别是角平分线,
∴∠1=$\frac{1}{2}$∠DAB,∠2=$\frac{1}{2}$∠ABE,
∴∠1+∠2=$\frac{1}{2}$×180°=90°,
∴∠C=180°-(∠1+∠2)=180°-90°=90°,
∴AC⊥BC,
∴同旁内角的平分线互相垂直,
故选A.
点评 本题考查了平行线的性质,用到的知识点是两直线平行,同旁内角互补,角平分线的定义,熟记性质是解题的关键,作出图形更形象直观.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
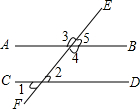 如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )| A. | 如果∠5=50°,那么AB∥CD | B. | 如果∠4=130°,那么AB∥CD | ||
| C. | 如果∠3=130°,那么AB∥CD | D. | 如果∠2=50°,那么AB∥CD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周零花钱的情况 | B. | 旅客上飞机前的安检 | ||
| C. | 工厂招聘工人,对应聘人员体检 | D. | 了解全国中小学生的身高情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
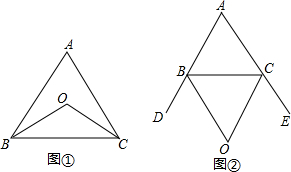
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
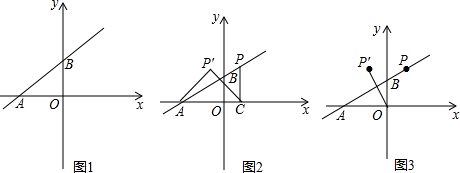
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com