
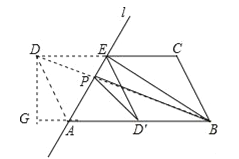
【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;
(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG,DG,根据勾股定理即可得到结论.
试题解析:(1)∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,∴四边形DAD′E是平行四边形,∴DE=AD′,∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC,∴CE=D′B,CE∥D′B,∴四边形BCED′是平行四边形;
∵AD=AD′,∴DAD′E是菱形,(2)∵四边形DAD′E是菱形,∴D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,∵CD∥AB,∴∠DAG=∠CDA=60°,∵AD=1,∴AG=![]() ,DG=
,DG=![]() ,∴BG=
,∴BG=![]() ,∴BD=
,∴BD=![]() =
=![]() ,∴PD′+PB的最小值为
,∴PD′+PB的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
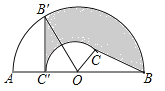
【题目】如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想测量教学楼的高度.他用一根绳子从楼顶垂下,发现绳子垂到地面后还多了2 m,当他把绳子的下端拉开6 m后,发现绳子下端刚好接触地面,则教学楼的高为___m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7…排列成如下的数表用十字框框出5个数(如图)
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2010吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于355吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.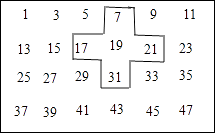
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:![]() .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店库存清仓,将最后两件羽绒服特价出售,甲款羽绒服卖出1200元,盈利20%,乙款羽绒服同样卖1200元,但亏损20%,该商店在这两笔交易中( )
A. 盈利100元 B. 亏损125元 C. 不赔不赚 D. 亏损100元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A. a:b:c =13∶5∶12 B. a2-b2=c2
C. a2=(b+c)(b-c) D. a:b:c=8∶16∶17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.![]()
解:∵AB=2cm,BC=2AB,
∴BC=4cm.
∴AC=AB+=cm.
∵D是AC的中点,
∴AD= ![]() =cm.
=cm.
∴BD=AD﹣=cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com