
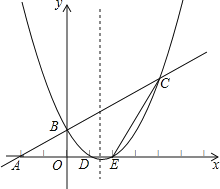
【题目】如图,已知一次函数y=![]() x+1的图象与x轴交于A点,与y轴交于B点:抛物线y=
x+1的图象与x轴交于A点,与y轴交于B点:抛物线y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
(1)求点B的坐标;
(2)求该抛物线的解析式;
(3)求四边形BDEC的面积S;
(4)在x轴上是否存在点P,使得以点P、B、C为顶点的三角形是直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)B(0,1);(2)y=![]() x2-
x2-![]() x+1;(3)4.5;(4)点P的坐标为(
x+1;(3)4.5;(4)点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(1,0)或(3,0).
,0)或(1,0)或(3,0).
【解析】
(1)在一次函数y=![]() x+1中,令x=0,即可求出点B的坐标;
x+1中,令x=0,即可求出点B的坐标;
(2)将点B、D的坐标代入二次函数解析式,求出b、c的值,即可求出二次函数的解析式;
(3)两解析式联立方程求得B、C的坐标,令y=![]() x2-
x2-![]() x+1=0,求得D、E的坐标,然后根据梯形和三角形的面积公式求得即可;
x+1=0,求得D、E的坐标,然后根据梯形和三角形的面积公式求得即可;
(4)设P(x,0),求得PB2=x2+1,PC2=(x-4)2+9,BC2=42+(3-1)2=20,然后分三种情况分别讨论求得即可.
(1)∵一次函数y=![]() x+1与y轴的交点为B,
x+1与y轴的交点为B,
令x=0,可得y=1,
∴B(0,1);
(2)将B(0,1),D(1,0)的坐标代入y=![]() x2+bx+c得,
x2+bx+c得,
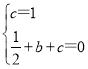 ,
,
解得: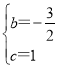 ,
,
∴解析式为:y=![]() x2-
x2-![]() x+1;
x+1;
(3)∵二次函数的图象与一次函数的图象交于B、C两点,
∴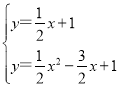 ,
,
解得:![]() ,
,![]() ,
,
∴C(4,3),
解![]() x2-
x2-![]() x+1=0,得x=1和x=2,
x+1=0,得x=1和x=2,
∴D(1,0),E(2,0),
∴S=![]() (1+3)×4-
(1+3)×4-![]() ×1×1-
×1×1-![]() (4-2)×3=4.5;
(4-2)×3=4.5;
(4)设P(x,0),
∵B(0,1),C(4,3),
∴PB2=x2+1,PC2=(x-4)2+9,BC2=42+(3-1)2=20,
①当∠PBC=90°时,则PB2+BC2=PC2,
即x2+1+20=(x-4)2+9,
解得x=![]() ,
,
∴P1(![]() ,0);
,0);
②当∠PCB=90°时,则PC2+BC2=PB2,
即x2+1=(x-4)2+9+20,
解得x=![]() ,
,
∴P2(![]() ,0);
,0);
③当∠BPC=90°时,则PB2+PC2=BC2,
即x2+1+(x-4)2+9=20,
解得x=1或x=3,
∴P3(1,0),P4(3,0);
∴在x轴上存在点P,使得以点P、B、C为顶点的三角形是直角三角形,点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(1,0)或(3,0).
,0)或(1,0)或(3,0).


科目:初中数学 来源: 题型:
【题目】已知函数![]() ,如表是函数的几组对应值:
,如表是函数的几组对应值:
x |
|
|
|
|
|
| 0 | 1 | 2 | 3 |
| 4 |
|
y |
|
|
|
|
|
| 0 |
|
|
|
|
|
|
请你根据学习函数的经验,利用表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究![]() 下面是小腾的探究过程,请补充完整.
下面是小腾的探究过程,请补充完整.
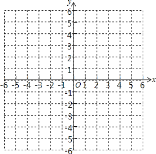
![]() 如图所示,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点
如图所示,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点![]() 根据描出的点,画出该函数的图象
根据描出的点,画出该函数的图象
![]() 根据函数图象,按要求填空:
根据函数图象,按要求填空:
![]() 在y轴左侧该函数图象有最______点,其坐标为______.
在y轴左侧该函数图象有最______点,其坐标为______.
![]() 当
当![]() 时,该函数y随x的增大而______.
时,该函数y随x的增大而______.
![]() 当方程
当方程![]() 只有一个解时,则a的取值范围为______.
只有一个解时,则a的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出200件.如果每件商品的售价每上涨2元,则每个月少卖5件,设每件商品的售价为x元,则可卖y件,每个月销售利润为w元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
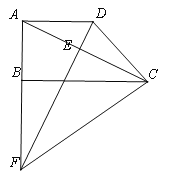
【题目】如图,已知梯形ABCD中,AD//BC ,∠ABC=90°,BC=2AB=8,对角线AC平分∠BCD,过点D作DE⊥AC,垂足为点E,交边AB的延长线于点F,联结CF.
(1)求腰DC的长;
(2)求∠BCF的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
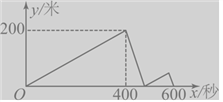
【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(2m+1)x2+4mx+2m﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数之和等于﹣1?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
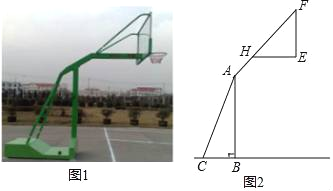
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com