
【题目】等腰直角三角形ABC中,∠BAC=90°,BD平分∠ABC交AC于点D,若AB+AD=8cm,则底边BC上的高为cm. 
【答案】4
【解析】解:作DE⊥BC于E, 因为BD平分∠ABC,根据角平分线上的点到角的两边的距离相等,
设AC=AB=x,则DE=AD=8﹣x,CD=x﹣(8﹣x),
在等腰直角三角形CDE中,根据勾股定理,
2(8﹣x)2=[x﹣(8﹣x)]2
解得x=4 ![]() ,
,
作BC边上的高AF,
AF=ABsin45°=4 ![]() ×
× ![]() =2×2=4,
=2×2=4,
则底边BC上的高为4cm.
所以答案是4.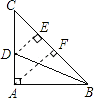
【考点精析】根据题目的已知条件,利用等腰直角三角形和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,
(1)AC=BC,∠ACB=90°,CD⊥AB,点E是AB边上一点,点F在线段CE上,且△CBF≌△EBF(如图①),求证:CE平分∠ACD; 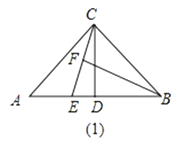
(2)除去(1)中条件“AC=BC”,其余条件不变(如图②),上述结论是否成立?并说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式的计算结果等于x2-5x-6的是( )
A. (x-6)(x+1) B. (x+6)(x-1)
C. (x-2)(x+3) D. (x+2)(x-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位![]() 得到直线
得到直线![]() ,
, ![]() 交
交![]() 轴于点D,交BC于点E,交抛物线于点F.
轴于点D,交BC于点E,交抛物线于点F.
(1)求点![]() ,点
,点![]() 和点
和点![]() 的坐标
的坐标
(2)如图2,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)在(2)的条件下,当点![]() 落在直线
落在直线![]() 上时,请直接写出点
上时,请直接写出点![]() 的坐标
的坐标

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com