
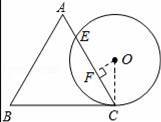
一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 cm.
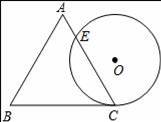

3 cm.
【考点】切线的性质;垂径定理;圆周角定理;弦切角定理.
【专题】几何图形问题.
【分析】连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边的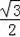
 倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为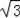
 ,即OC=
,即OC=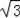
 ,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
【解答】解:连接OC,并过点O作OF⊥CE于F,
且△ABC为等边三角形,边长为4,
故高为2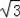
 ,即OC=
,即OC=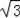
 ,
,
又∠ACB=60°,故有∠OCF=30°,
在Rt△OFC中,可得FC=OC•cos30°=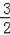
 ,
,
OF过圆心,且OF⊥CE,根据垂径定理易知CE=2FC=3.
故答案为:3.

【点评】本题主要考查了切线的性质和等边三角形的性质和解直角三角形的有关知识.题目不是太难,属于基础性题目.


科目:初中数学 来源: 题型:
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于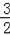
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
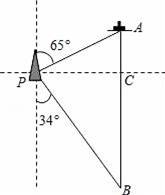
如图,一艘海伦位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海伦所在的B处距离灯塔P有多远?(sin65°≈0.91,cos65°≈0.42,sin34°≈0.56,cos34°≈0.83)

查看答案和解析>>
科目:初中数学 来源: 题型:
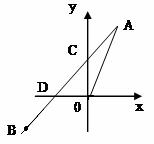
如图正比例函数y=2x的图像与一次函数 y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1)与y轴交点为C与x轴交点为D.
 (1)求一次函数的解析式;
(1)求一次函数的解析式;
(2)求C点的坐标;
(3)求△AOD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com