
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于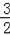
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
B【考点】二次函数的性质.
【专题】压轴题;新定义.
【分析】①当m=﹣3时,根据函数式的对应值,可直接求顶点坐标;②当m>0时,直接求出图象与x轴两交点坐标,再求函数图象截x轴所得的线段长度,进行判断;③当m<0时,根据对称轴公式,进行判断;④当m≠0时,函数图象经过同一个点.
【解答】解:根据定义可得函数y=2mx2+(1﹣m)x+(﹣1﹣m),
①当m=﹣3时,函数解析式为y=﹣6x2+4x+2,
∴
 =﹣
=﹣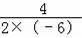
 =
=
 ,
,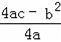
 =
=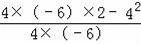
 =
=
 ,
,
∴顶点坐标是(
 ,
,
 ),正确;
),正确;
②函数y=2mx2+(1﹣m)x+(﹣1﹣m)与x轴两交点坐标为(1,0),(﹣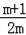
 ,0),
,0),
当m>0时,1﹣(﹣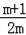
 )=
)=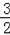
 +
+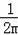
 >
>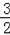
 ,正确;
,正确;
③当m<0时,函数y=2mx2+(1﹣m)x+(﹣1﹣m)开口向下,对称轴x=
 ﹣
﹣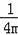
 >
>
 ,
,
∴x可能在对称轴左侧也可能在对称轴右侧,错误;
④y=2mx2+(1﹣m)x+(﹣1﹣m)=m(2x2﹣x﹣1)+x﹣1,若使函数图象恒经过一点,m≠0时,应使2x2﹣x﹣1=0,可得x1=1,x2=﹣
 ,当x=1时,y=0,当x=﹣
,当x=1时,y=0,当x=﹣
 时,y=﹣
时,y=﹣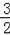
 ,则函数一定经过点(1,0)和(﹣
,则函数一定经过点(1,0)和(﹣
 ,﹣
,﹣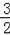
 ),正确.
),正确.
故选B.
【点评】公式法:y=ax2+bx+c的顶点坐标为(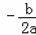
 ,
,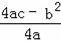
 ),对称轴是x=
),对称轴是x=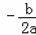
 .
.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
把2016个正整数1,2,3,4,…,2016按如图方式排列成如图所示的数的方阵.
(1)如图,用一个正方形框,在表中任意框住4个数,记左上角的一个数为x,另三个数x的代数式表示,则从小到大依次是 , , .
(2)当(1)中被框住的4个数之和等于2016时,x的值为多少?
(3)在(1)中能否框住这样的4个数,使它们的和等于2015,等于2032.若能,求出x的值;若不能,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
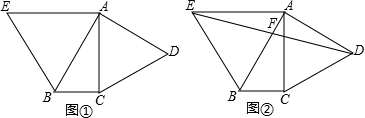
已知,Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以AB,AC为边在△ABC外侧作等边三角形ABE与等边三角形ACD.
(1)如图①,求∠BAD的大小;
(2)如图②,连接DE交AB于点F.求证:EF=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
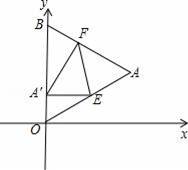
如图,△OAB是边长为2+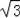
 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=﹣
 x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
一个射手连续射靶22次,其中三次射中10环,7次射中9环,9次射中8环,3次射中7环,则射中环数的中位数和众数分别为
A.8,9 B.8,8 C.8.5,8 D.8.5,9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com