
如图,△OAB是边长为2+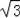
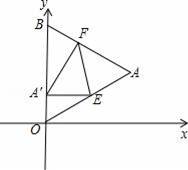
 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=﹣
 x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.

【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)当A′E∥x轴时,△A′EO是直角三角形,可根据∠A′OE的度数用O′A表示出OE和A′E,由于A′E=AE,且A′E+OE=OA=2+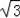
 ,由此可求出OA′的长,也就能求出A′E的长.据此可求出A′和E的坐标;
,由此可求出OA′的长,也就能求出A′E的长.据此可求出A′和E的坐标;
(2)将A′,E点的坐标代入抛物线中,即可求出其解析式.进而可求出抛物线与x轴的交点坐标;
(3)根据折叠的性质可知:∠FA′E=∠A,因此∠FA′E不可能为直角,因此要使△A′EF成为直角三角形只有两种可能:
①∠A′EF=90°,根据折叠的性质,∠A′EF=∠AEF=90°,此时A′与O重合,与题意不符,因此此种情况不成立.
②∠A′FE=90°,同①,可得出此种情况也不成立.
因此A′不与O、B重合的情况下,△A′EF不可能成为直角三角形.
【解答】解:(1)由已知可得∠A′OE=60°,A′E=AE,
由A′E∥x轴,得△OA′E是直角三角形,
设A′的坐标为(0,b),
AE=A′E=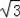
 b,OE=2b,
b,OE=2b,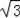
 b+2b=2+
b+2b=2+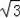
 ,
,
所以b=1,A′、E的坐标分别是(0,1)与(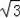
 ,1).
,1).
(2)因为A′、E在抛物线上,
所以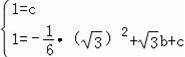
 ,
,
所以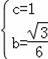
 ,
,
函数关系式为y=﹣
 x2+
x2+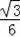
 x+1,
x+1,
由﹣
 x2+
x2+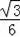
 x+1=0,
x+1=0,
得x1=﹣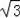
 ,x2=2
,x2=2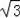
 ,
,
与x轴的两个交点坐标分别是(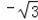
 ,0)与(
,0)与(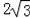
 ,0).
,0).
(3)不可能使△A′EF成为直角三角形.
∵∠FA′E=∠FAE=60°,
若△A′EF成为直角三角形,只能是∠A′EF=90°或∠A′FE=90°
若∠A′EF=90°,利用对称性,则∠AEF=90°,
A、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A′FE=90°也不可能,
所以不能使△A′EF成为直角三角形.
【点评】本题着重考查了待定系数法求二次函数解析式、图形旋转变换、直角三角形的判定和性质等知识点,综合性较强.


科目:初中数学 来源: 题型:
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于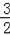
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
解不等式组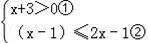

请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得
(Ⅱ)解不等式②,得
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
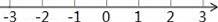

查看答案和解析>>
科目:初中数学 来源: 题型:
为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
(1) 请将条形统计图补充完整;
(2) 求这100个样本数据的平均数,众数和中位数;
(3) 根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com