
把2016个正整数1,2,3,4,…,2016按如图方式排列成如图所示的数的方阵.
(1)如图,用一个正方形框,在表中任意框住4个数,记左上角的一个数为x,另三个数x的代数式表示,则从小到大依次是 , , .
(2)当(1)中被框住的4个数之和等于2016时,x的值为多少?
(3)在(1)中能否框住这样的4个数,使它们的和等于2015,等于2032.若能,求出x的值;若不能,说明理由.


【考点】一元一次方程的应用.
【分析】(1)根据表格分别找出左右、上下相邻的两个数字之间的数量关系从而得到答案;
(2)根据这四个数的和为2016列方程求解即可;
(3)先根据它们的和等于2015和2032,然后计算出x的值,最后再x为正整数、x不能为每一行的最后一个数字判断即可.
【解答】解:(1)记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是x+1,x+7,x+8.
故答案为:x+1;x+7,;x+8.
(2)根据题意可得:x+(x+1)+(x+7)+(x+8)=2016,
解得:x=500
答:x的值是500.
(3)不能.
假设能框住这样的4个数,它们的和等于2015,
则x+(x+1)+(x+7)+(x+8)=2015,
解得:x=499.75,
因为不是整数,不符合题意,因而不能.
假设能框住这样的4个数,它们的和等于2032,
则x+(x+1)+(x+7)+(x+8)=2032,
解得:x=504,
因为504,505,511,512不在同一个正方形框内,不符合题意,因而不能.
【点评】本题主要考查的是一元一次方程的应用,判断出504,505,511,512不在同一个正方形框内是解题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x﹣y)2=x2﹣2xy﹣y2
C.(x+2y)(x﹣2y)=x2﹣2y2 D.(﹣x+y)2=x2﹣2xy+y2
查看答案和解析>>
科目:初中数学 来源: 题型:
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于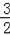
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com