
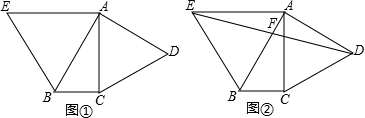
已知,Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以AB,AC为边在△ABC外侧作等边三角形ABE与等边三角形ACD.
(1)如图①,求∠BAD的大小;
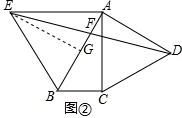
(2)如图②,连接DE交AB于点F.求证:EF=DF.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质得到∠CAD=60°,由∠BAC=30°,根据角的和差关系,于是得到结论;
(2)作EG∥AD,交AB于点G,由等边三角形的∠DAC=60°,加上已知的∠CAB=30°得到∠FAD=90°,然后根据两直线平行内错角相等得到∠EGF=90°,再根据∠ACB=90°,∠CAB=30°,利用三角形的内角和定理得到∠ABC=60°,由等边三角形的性质也得到∠EBG=60°,从而得到两角相等,再由EB=AB,利用“AAS”证得△EGB≌△ACB,根据全等三角形的对应边相等得到EG=AC,再由△ADC为等边三角形得到AD=AC,等量代换可得EG=AD,加上一对对顶角的相等和一对直角的相等,根据“AAS”证得△EGF≌△DAF,最后根据全等三角形的对应边相等即可得证.
【解答】(1)解:∵△ACD是等边三角形,
∴∠CAD=60°,
∵∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=90°;
(2)证明:如图②,作EG∥AD,交AB于点G,
由∠DAC=60°,∠CAB=30°得:∠FAD=∠DAC+∠CAB=90°,
∴∠EGF=∠FAD=90°,
又∵∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
又∵△ABE为等边三角形,∠EBG=60°,EB=AB,
∴∠EBG=∠ABC=60°,
在△EGB和△ACB中,
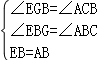 ,
,
∴△EGB≌△ACB(AAS),
∴EG=AC,
又∵△ADC为等边三角形,
∴AD=AC,
∴EG=AD,
在△EGF和△DAF中,
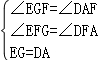 ,
,
∴△EGF≌△DAF(AAS),
∴EF=DF,即F为DE中点.
【点评】此题考查了全等三角形的判定与性质,平行线的性质,以及等边三角形的性质,其中全等三角形的判定方法为:SSS;SAS;ASA;AAS;HL(直角三角形判定全等的方法),常常利用三角形的全等来解决线段或角相等的问题,在证明三角形全等时,要注意公共角及公共边,对顶角相等等隐含条件的运用.第二问作出辅助线构造全等三角形是本问的突破点.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
下列计算正确的是( )
A.(x+y)2=x2+y2 B.(x﹣y)2=x2﹣2xy﹣y2
C.(x+2y)(x﹣2y)=x2﹣2y2 D.(﹣x+y)2=x2﹣2xy+y2
查看答案和解析>>
科目:初中数学 来源: 题型:
定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:
①当m=﹣3时,函数图象的顶点坐标是(
 ,
,
 );
);
②当m>0时,函数图象截x轴所得的线段长度大于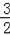
 ;
;
③当m<0时,函数在x>
 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过同一个点.
其中正确的结论有( )
A.①②③④ B.①②④ C.①③④ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com