
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)分别求出直线![]() 、直线
、直线![]() 的表达式;
的表达式;
(2)在直线![]() 上是否存在一点P,使得
上是否存在一点P,使得![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
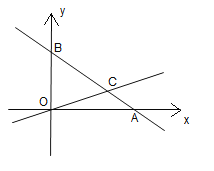
【答案】(1)直线OC表达式: ![]() ;直线AB表达式:
;直线AB表达式: ![]() ;(2)P的坐标(3,2)或(﹣3,6)
;(2)P的坐标(3,2)或(﹣3,6)
【解析】
(1)利用待定系数法求出各表达式即可.
(2)先根据题目的条件解出S△OCP,再设出P点横坐标代入求出,再将横坐标代入AB表达式即可.
(1)设直线OC的表达式为:y=kx,
将![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线OC的表达式为: ![]() .
.
∵AB过点(0,4),设直线AB的表达式为:y=kx+4,
将![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为: ![]() .
.
(2) 存在, P的坐标为(3,2)或(﹣3,6),理由如下:
![]() ,
,
设P点横坐标Px,则![]() ,
,
解得Px=±3,
将x=3代入![]() ,解得y=2,
,解得y=2,
将x=﹣3代入![]() ,解得y=6,
,解得y=6,
∴P的坐标为(3,2)或(﹣3,6).


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
【题目】如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是( )
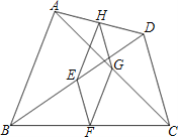
A.四边形EFGH一定是平行四边形B.当AB=CD时,四边形EFGH是菱形
C.当AC⊥BD时,四边形EFGH是矩形D.四边形EFGH可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
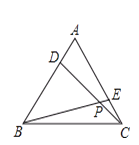
【题目】如图,已知:在等边△ABC中,D、E分别在AB、AC上,且AD=CE,BE、CD相交于点P.
(1)说明△ADC≌△CEB的理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )

A. 10cm B. ![]() C.
C. ![]() D. 9cm
D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
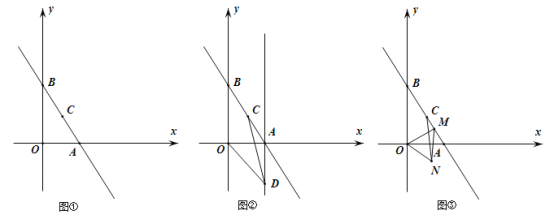
(1)如图①,点![]() 的坐标为( , ),点
的坐标为( , ),点![]() 的坐标为( , ),
的坐标为( , ),![]()
![]() ;
;
(2)如图②,若点![]() 是经过点
是经过点![]() ,且与
,且与![]() 轴平行的直线上的一个动点,求
轴平行的直线上的一个动点,求![]() 的最小值;
的最小值;
(3)如图③,点![]() 是线段
是线段![]() 上一动点,以
上一动点,以![]() 为边在
为边在![]() 的下方作等边
的下方作等边![]() ,连接
,连接![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
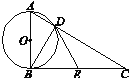
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,E是BC的中点,连接BD,DE.
(1)若![]() ,求sinC;
,求sinC;
(2)求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com