练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是正方形，△EBC是等边三角形，则∠AED的度数为_________．

    【答案】150

    【解析】

    根据题意先得出AB=BC=BE,EC=BC=DC,并以此求出∠AEB 和∠DEC，进而利用∠AED=360°-∠AEB -∠DEC -∠BEC即可求出∠AED的度数．

    解：∵四边形ABCD是正方形，△EBC是等边三角形，

    ∴AB=BC=BE,EC=BC=DC, ∠ABE=∠DCE=90°-60°=30°，

    ∴∠AEB=∠EAB=（180°-30°）÷2=75°，

    ∴∠DEC=∠EDC=（180°-30°）÷2=75°，

    ∴∠AED=360°-∠AEB -∠DEC -∠BEC =360°-75°-75°-60°=150°．

    故答案为：150°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

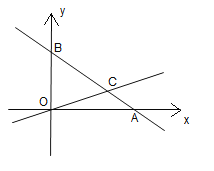
    【题目】如图，在平面直角坐标系中，过点的直线与直线相交于点．

    （1）分别求出直线、直线的表达式；

    （2）在直线上是否存在一点P，使得？若存在，求出此时点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

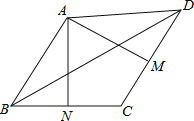
    【题目】在四边形ABCD中，M、N分别是CD、BC的中点， 且AM⊥CD，AN⊥BC，已知∠MAN=74°，∠DBC=41°，则∠ADB度数为（ ）．

    A.15°B.17°

    C.16°D.32°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于O点，且BE=BF，∠BEF=2∠BAC。

    （1）求证：OE=OF；

    （2）若BC=，求AB的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知是的外角的平分线，且交的延长线于点．

    （1）若恰好垂直平分，求的度数；

    （2）王涵探究后提出等式：，请通过证明判断“王涵发现”是否正确；

    （3）如图②，过点作，垂足为，若，，求的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，∠DAB=60°，AB=2AD，点E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G．

    （1）求证：四边形DEBF是菱形；

    （2）请判断四边形AGBD是什么特殊四边形? 并加以证明；

    （3）若AD=1，求四边形AGCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a、b，那么 的值为（ ）.

    A. 49 B. 25 C. 13 D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

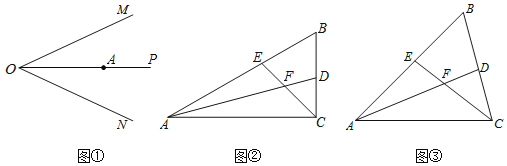
    【题目】（1）如图①，OP是∠MON的平分线，点A为OP上一点，请你作一个∠BAC，B、C分别在OM、ON上，且使AO平分∠BAC（保留作图痕迹）；

    （2）如图②，在△ABC中，∠ACB是直角，∠B＝60°，△ABC的平分线AD，CE相交于点F，请你判断FE与FD之间的数量关系（可类比（1）中的方法）；

    （3）如图③，在△ABC中，如果∠ACB≠90°，而（2）中的其他条件不变，请问（2）中所得的结论是否仍然成立？若成立，请证明，若不成立，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某水果店进行了一次促销活动，一次性购买种水果的单价（元）与购买量（千克）的函数关系如图．

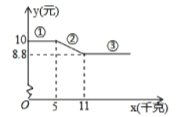
    （1）当时，单价为_______元．

    （2）求图中第②段函数图象的解析式，并指出的取值范围．

    （3）促销活动期间，张老师计划去该店买种水果10千克，那么张老师共需花费多少钱？

    查看答案和解析>>

    同步练习册答案